| Codeforces Round 788 (Div. 2) |
|---|
| Закончено |
В последнем региональном соревновании Хемос со своей командой наконец-то отобрались на Финал ICPC, поэтому в честь этого достижения, а также из-за любви к деревьям он предлагает вам эту задачу, одноименную его команде «Hemose 3al shagra» (Хемос на дереве).
Вам дано дерево из $$$n$$$ вершин, где $$$n$$$ — степень $$$2$$$. Вам нужно назначить каждой вершине и каждому ребру целое число из диапазона $$$[1,2n -1]$$$ (включительно) так, чтобы все значения были различны.
После назначения вы должны выбрать одну из вершин дерева в качестве корня так, чтобы максимальная стоимость среди всех простых путей от корня до всех вершин или ребер была минимально возможная.
Стоимость пути между двумя вершинами $$$u$$$ и $$$v$$$ или между вершиной $$$u$$$ и ребром $$$e$$$ определяется как побитовое исключающее ИЛИ всех значений вершин и ребер на пути между ними, включая концы (обратите внимание, что в дереве есть только один простой путь между парой вершин или вершиной и ребром).
Первая строка содержит одно целое число $$$t$$$ ($$$1 \le t \le 5\cdot 10^4$$$) — количество наборов входных данных. Далее следуют $$$t$$$ наборов входных данных.
Первая строка каждого набора содержит одно целое число $$$p$$$ ($$$1 \le p \le 17$$$), где $$$n$$$ (количество вершин в дереве) равно $$$2^p$$$.
Каждая из следующих $$$n−1$$$ строк содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u,v \le n$$$), обозначающих ребро между вершинами $$$u$$$ и $$$v$$$ в дереве.
Гарантируется, что данный граф образует дерево.
Гарантируется, что сумма значений $$$n$$$ по всем наборам входных данных не превосходит $$$3\cdot 10^5$$$.
Для каждого набора входных данных выведите в первой строке выбранный корень.
Во второй строке выведите $$$n$$$ целых чисел, где $$$i$$$-е число обозначает значение, выбранное для $$$i$$$-й вершине.
В третьей строке выведите $$$n-1$$$ целое число, где $$$i$$$-е число обозначает значение выбранное для $$$i$$$-го ребра. Ребра нумеруются в порядке присутствия во входных данных
Если существует несколько решений, выведите любое из них.
221 22 33 431 22 33 41 51 65 75 8
3 5 1 3 6 4 2 7 5 1 2 8 11 4 13 9 15 6 14 3 7 10 5 12
Дерево в первом наборе входных данных показано ниже.
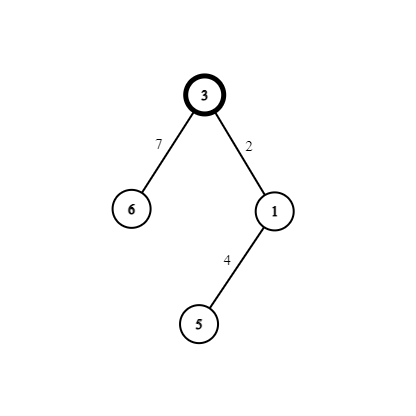
Стоимости путей следующие:
- $$$3$$$;
- $$$3\oplus 7=4$$$;
- $$$3\oplus 7\oplus 6=2$$$;
- $$$3\oplus 2=1$$$;
- $$$3\oplus 2\oplus 1=0$$$;
- $$$3\oplus 2\oplus 1\oplus 4=4$$$;
- $$$3\oplus 2\oplus 1\oplus 4\oplus 5=1$$$.
Максимальная стоимость равна $$$4$$$. Можно показать, что не существует способа расставить числа и выбрать корень так, чтобы получилась меньшая максимальная стоимость.
Дерево для второго набора показано ниже:
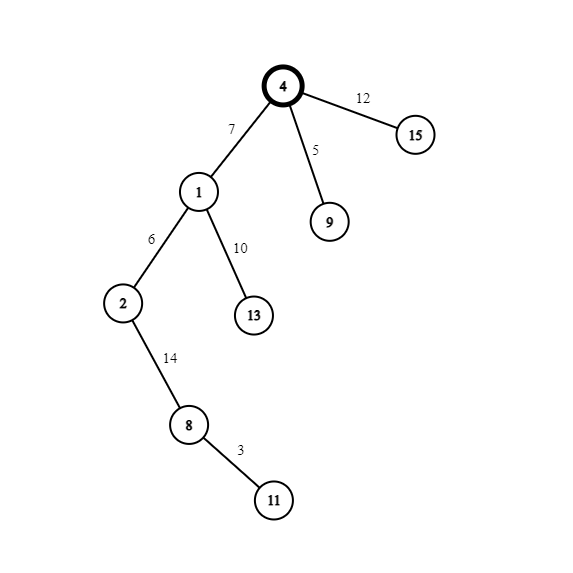
| Название |
|---|




