| Codeforces Round 791 (Div. 2) |
|---|
| Закончено |
Однажды Маша прогуливалась по парку и нашла под деревом граф... Удивлены? Вы думали, что в этой задаче будет логичная обоснованная история? Не дождетесь! Так вот...
У Маши есть ориентированный граф, в $$$i$$$-й вершине которого записано некоторое целое положительное число $$$a_i$$$. Изначально Маша может положить в некоторую вершину графа монетку. За один ход разрешается переместить монетку, которая сейчас находится в некоторой вершине $$$u$$$, в любую вершину $$$v$$$, такую что в графе существует ориентированное ребро $$$u \to v$$$. Каждый раз, когда монетка оказывается в какой-либо вершине $$$i$$$, Маша записывает в блокнот число $$$a_i$$$ (в частности, когда Маша изначально кладет монетку в некоторую вершину графа, она пишет в блокнот число, записанное в этой вершине). Маша хочет сделать ровно $$$k - 1$$$ ходов таким образом, чтобы максимальное число, записанное ей в блокноте, было как можно меньше.
Первая строка содержит три целых числа $$$n$$$, $$$m$$$ и $$$k$$$ ($$$1 \le n \le 2 \cdot 10^5$$$, $$$0 \le m \le 2 \cdot 10^5$$$, $$$1 \le k \le 10^{18}$$$) — количество вершин и ребер в графе, а также количество ходов, которое хочет сделать Маша, соответственно.
Вторая строка содержит $$$n$$$ целых чисел $$$a_i$$$ ($$$1 \le a_i \le 10^9$$$) — числа, записанные в вершинах графа.
Каждая из следующих $$$m$$$ строк содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u \ne v \le n$$$) — это означает, что в графе существует ребро $$$u \to v$$$.
Гарантируется, что граф не содержит петель и кратных ребер.
Выведите одно целое число — минимальное значение максимального числа, которое Маша выписала в блокнот, при оптимальном перемещении монетки.
В случае, если Маше не удастся переместить монетку $$$k - 1$$$ раз, в качестве ответа выведите число $$$-1$$$.
6 7 4 1 10 2 3 4 5 1 2 1 3 3 4 4 5 5 6 6 2 2 5
4
6 7 100 1 10 2 3 4 5 1 2 1 3 3 4 4 5 5 6 6 2 2 5
10
2 1 5 1 1 1 2
-1
1 0 1 1000000000
1000000000
На изображении ниже приведен граф, описанный в первых двух примерах.
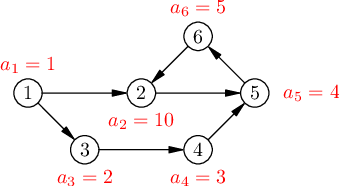
В первом примере можно выбрать в качестве изначальной вершину $$$1$$$. После этого можно выполнить три хода: $$$1 \to 3$$$, $$$3 \to 4$$$ и $$$4 \to 5$$$. В итоге в блокнот будут записаны числа $$$1, 2, 3$$$ и $$$4$$$.
Во втором примере можно выбрать в качестве изначальной вершину $$$2$$$. После этого можно выполнить $$$99$$$ ходов: $$$2 \to 5$$$, $$$5 \to 6$$$, $$$6 \to 2$$$, $$$2 \to 5$$$, и так далее. В итоге в блокнот будут записаны числа $$$10, 4, 5, 10, 4, 5, \ldots, 10, 4, 5, 10$$$.
В третьем примере на имеющемся графе не удастся выполнить $$$4$$$ хода.
| Название |
|---|




