| Codeforces Round 793 (Div. 2) |
|---|
| Закончено |
Дано $$$n$$$ вершин, расположенных на окружности, пронумерованных от $$$1$$$ до $$$n$$$ по часовой стрелке. Вам также дана бинарная строка $$$s$$$ длины $$$n$$$.
Ваша задача — построить дерево на заданных $$$n$$$ вершинах, удовлетворяющее двум условиям ниже, или сообщить, что такого дерева не существует:
- Для каждой вершины $$$i$$$ $$$(1 \le i \le n)$$$, степень вершины четная, если $$$s_i = 0$$$ и нечетная, если $$$s_i = 1$$$.
- Никакие два ребра дерева не пересекаются внутри окружности. Разрешается, чтобы ребра пересекались на окружности.
Обратите внимание, что все ребра рисуются как отрезки прямых линий. Например, ребро $$$(u, v)$$$ в дереве рисуется как отрезок прямой, соединяющий $$$u$$$ и $$$v$$$ на окружности.
Дерево с $$$n$$$ вершинами — это связный граф с $$$n - 1$$$ ребрами.
Входные данные состоят из нескольких наборов входных данных. Первая строка содержит одно целое число $$$t$$$ $$$(1 \leq t \leq 2\cdot 10^4)$$$ — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ $$$(2 \leq n \leq 2\cdot 10^5)$$$ — количество вершин.
Вторая строка каждого набора входных данных содержит бинарную строку $$$s$$$ длины $$$n$$$.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превышает $$$2\cdot 10^5$$$.
Для каждого набора входных данных, если не существует дерева, удовлетворяющего заданным условиям, выведите «NO» (без кавычек), иначе выведите «YES», а затем выведите описание дерева.
Вы можете выводить каждую букву в любом регистре (например, «YES», «Yes», «yes», «yEs», «yEs» будут распознаны как положительный ответ).
Если существует дерево, то выведите $$$n - 1$$$ строк, каждая из которых содержит два целых числа $$$u$$$ и $$$v$$$ $$$(1 \leq u,v \leq n, u \neq v)$$$, обозначающих ребро между $$$u$$$ и $$$v$$$ в дереве. Если существует несколько возможных ответов, выведите любой из них.
3401102106110110
YES 2 1 3 4 1 4 NO YES 2 3 1 2 5 6 6 2 3 4
В первом наборе входных данных дерево выглядит следующим образом:
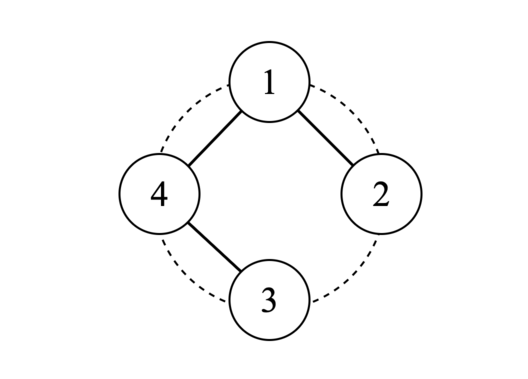
Во втором наборе входных данных существует только одно возможное дерево с ребром между $$$1$$$ и $$$2$$$, и оно не удовлетворяет ограничениям на степени.
В третьем наборе входных данных,
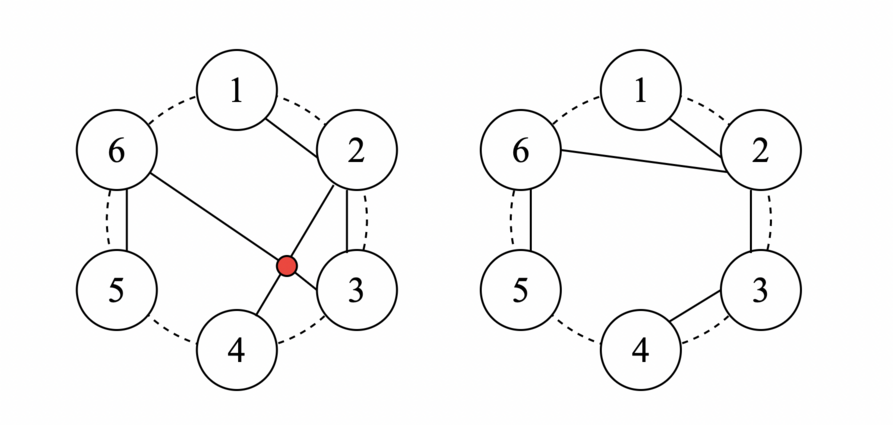
| Название |
|---|




