| Codeforces Round 798 (Div. 2) |
|---|
| Закончено |
Байтландия — прекрасная земля, известная своими красивыми деревьями.
Миша нашел бинарное дерево с $$$n$$$ вершинами, пронумерованными от $$$1$$$ до $$$n$$$. Бинарное дерево — это ациклический связный неориентированный граф, содержащий $$$n$$$ вершин и $$$n - 1$$$ ребер. Каждая вершина имеет степень не больше $$$3$$$, а корнем является вершина с номером $$$1$$$ и имеет степень не больше $$$2$$$.
К сожалению, корень дерева был заражен. Следующий процесс происходит $$$n$$$ раз:
- Миша либо выбирает еще не зараженную (и не удаленную) вершину и удаляет ее со всеми ребрами, имеющими конец в этой вершине, либо ничего не делает.
- Затем заражение распространяется на каждую вершину, соединенную ребром с уже зараженной вершиной (все уже зараженные вершины остаются зараженными).
Так как Мише некогда думать, скажите ему, какое максимальное количество вершин он может спасти от заражения (обратите внимание, что удаленные вершины не считаются спасенными).
Во входных данных находятся несколько наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1\leq t\leq 5000$$$) — количество наборов входных данных. Далее следуют наборы входных данных.
В первой строке каждого набора задано одно целое число $$$n$$$ ($$$2\leq n\leq 3\cdot 10^5$$$) — количество вершин дерева.
В $$$i$$$-й из следующих $$$n-1$$$ строк набора входных данных задано два числа $$$u_i$$$ и $$$v_i$$$ ($$$1 \leq u_i, v_i \leq n$$$), обозначающих очередное ребро дерева.
Гарантируется, что граф является бинарным деревом с корнем в вершине $$$1$$$. Также гарантируется, что сумма $$$n$$$ по всем наборам не превышает $$$3\cdot 10^5$$$.
Для каждого набора входных данных выведите единственное целое число — ответ на задачу.
421 241 22 32 471 21 52 32 45 65 7151 22 33 44 54 63 72 81 99 109 1110 1210 1311 1411 15
0 2 2 10
В первом наборе входных данных единственным возможным действием является удаление вершины $$$2$$$, после чего мы спасли $$$0$$$ вершин.
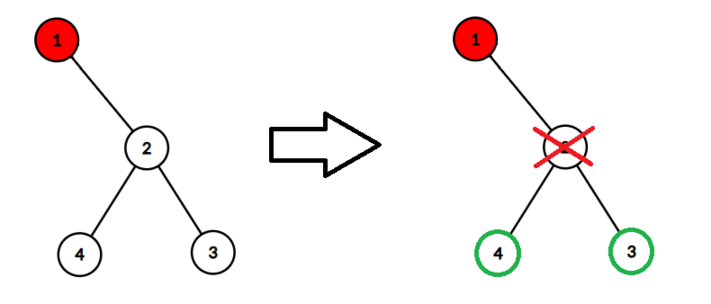
Во втором наборе входных данных, если мы удалим вершину $$$2$$$, мы сможем спасти вершины $$$3$$$ и $$$4$$$.
| Название |
|---|




