Вам дано $$$n$$$ цветных отрезков на числовой оси. Каждый отрезок либо красный, либо синий. Отрезок $$$i$$$ описывается тройкой чисел $$$(c_i, l_i, r_i)$$$. Отрезок содержит все точки на отрезке $$$[l_i, r_i]$$$, включая концы, а его цвет описывается значением $$$c_i$$$:
- если $$$c_i = 0$$$, то это красный отрезок;
- если $$$c_i = 1$$$, то это синий отрезок.
Скажем, что два отрезка различных цветов соединены, если они имеют хотя бы одну общую точку. Два отрезка принадлежат одной группе отрезков, если они соединены непосредственно или через цепочку соединенных непосредственно отрезок. Найдите число различных групп отрезков.
Во входных данных находятся несколько наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 10^5$$$) — количество наборов входных данных. Далее следуют наборы входных данных.
Первая строка набора входных данных содержит одно целое число $$$n$$$ ($$$1 \leq n \leq 10^5$$$) — количество отрезков.
Каждая из следующих $$$n$$$ строк содержит три целых числа $$$c_i, l_i, r_i$$$ ($$$0 \leq c_i \leq 1, 0 \leq l_i \leq r_i \leq 10^9$$$), описывающие $$$i$$$-й отрезок.
Гарантируется, что сумма значений $$$n$$$ по всем наборам входных данных не превосходит $$$10^5$$$.
Для каждого набора входных данных выведите одно целое число $$$k$$$ — количество групп отрезков.
250 0 51 2 120 4 71 9 160 13 1931 0 11 1 20 3 4
2 3
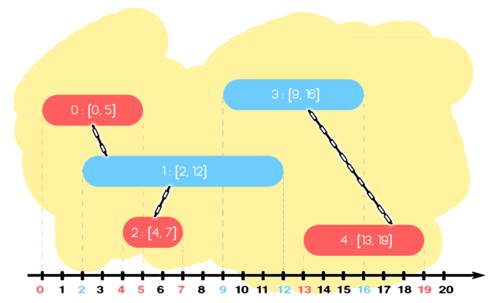
В первом примере $$$5$$$ отрезков. Отрезки $$$1$$$ и $$$2$$$ соединены, так как они различных цветов и имеют общую точку. Также отрезки $$$2$$$ и $$$3$$$ соединены, и отрезки $$$4$$$ и $$$5$$$ соединены. Таким образом, есть две группы: одна содержит отрезки $$$\{1, 2, 3\}$$$, другая содержит отрезки $$$\{4, 5\}$$$.
| Название |
|---|




