Вам дано дерево $$$G$$$ из $$$n$$$ вершин, а также целое число $$$k$$$. Вершины дерева пронумерованы от $$$1$$$ до $$$n$$$.
Для некоторой вершины $$$r$$$ и подмножества $$$S$$$ вершин дерева $$$G$$$ такого, что $$$|S| = k$$$, определим $$$f(r, S)$$$ как размер наименьшего корневого поддерева, содержащего все вершины $$$S$$$ при условии, что корнем дерева является вершина $$$r$$$. Множество вершин $$$T$$$ называется корневым поддеревом, если все вершины в $$$T$$$ связны и для любой вершины в $$$T$$$ все ее потомки тоже принадлежат $$$T$$$.
Вам нужно вычислить сумму $$$f(r, S)$$$ по всем различным комбинациям вершины $$$r$$$ и подмножества $$$S$$$, где $$$|S| = k$$$. Формально, вычислите следующее: $$$$$$\sum_{r \in V} \sum_{S \subseteq V, |S| = k} f(r, S),$$$$$$ где $$$V$$$ — множество вершин дерева $$$G$$$.
Выведите ответ по модулю $$$10^9 + 7$$$.
Первая строка содержит два целых числа $$$n$$$ и $$$k$$$ ($$$3 \le n \le 2 \cdot 10^5$$$, $$$1 \le k \le n$$$).
Каждая из следующих $$$n - 1$$$ строк содержит два целых числа $$$x$$$ и $$$y$$$ ($$$1 \le x, y \le n$$$), обозначающих ребро между вершинами $$$x$$$ и $$$y$$$.
Гарантируется, что данные ребра образуют дерево.
Выведите ответ по модулю $$$10^9 + 7$$$.
3 2 1 2 1 3
25
7 2 1 2 2 3 2 4 1 5 4 6 4 7
849
Дерево во втором примере показано ниже:
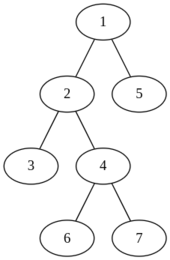
Всего в этом дереве $$$21$$$ подмножество вершин размера $$$2$$$. А именно, $$$$$$S \in \left\{\{1, 2\}, \{1, 3\}, \{1, 4\}, \{1, 5\}, \{1, 6\}, \{1, 7\}, \{2, 3\}, \{2, 4\}, \{2, 5\}, \{2, 6\}, \{2, 7\}, \{3, 4\}, \{3, 5\}, \{3, 6\}, \{3, 7\}, \{4, 5\}, \{4, 6\}, \{4, 7\}, \{5, 6\}, \{5, 7\}, \{6, 7\} \right\}.$$$$$$ Так как в дереве $$$7$$$ вершин, $$$1 \le r \le 7$$$. Нужно найти сумму $$$f(r, S)$$$ по всем парам $$$r$$$ и $$$S$$$.
Ниже перечислены значения $$$f(r, S)$$$ для некоторых комбинаций $$$r$$$ и $$$S$$$.
- $$$r = 1$$$, $$$S = \{3, 7\}$$$. Значение $$$f(r, S)$$$ равно $$$5$$$, а соответствующее поддерево равно $$$\{2, 3, 4, 6, 7\}$$$.
- $$$r = 1$$$, $$$S = \{5, 4\}$$$. Значение $$$f(r, S)$$$ равно $$$7$$$, а соответствующее поддерево равно $$$\{1, 2, 3, 4, 5, 6, 7\}$$$.
- $$$r = 1$$$, $$$S = \{4, 6\}$$$. Значение $$$f(r, S)$$$ равно $$$3$$$, а соответствующее поддерево равно $$$\{4, 6, 7\}$$$.
| Название |
|---|




