Поликарп и Монокарп решают одну и ту же головоломку с домино. Им дан одинаковый набор из $$$n$$$ доминошек, $$$i$$$-я из которых содержит два числа $$$x_i$$$ и $$$y_i$$$. Также им обоим дана одинаковая таблица $$$m$$$ на $$$k$$$ с числами $$$a_{ij}$$$ такая, что $$$m\cdot k = 2n$$$.
Задача состоит в том, чтобы разместить $$$n$$$ доминошек на таблице таким образом, чтобы никакие две из них не пересекались, а значения на каждой доминошке совпадали со значениями $$$a_{ij}$$$, которые покрывает доминошка. Домино можно произвольно поворачивать перед размещением на таблице, поэтому домино $$$(x_i, y_i)$$$ эквивалентно домино $$$(y_i, x_i)$$$.
Они оба решили головоломку и сравнили свои ответы, но заметили, что их решения не только не совпадают, но ни одна из $$$n$$$ доминошек не находится в одном и том же месте в обоих решениях! Формально, если в решении Поликарпа две ячейки были покрыты одной и той же доминошкой, то в решении Монокарпа они были покрыты разными доминошками. На изображении ниже показана одна потенциальная таблица $$$a$$$, а также решения двух игроков.
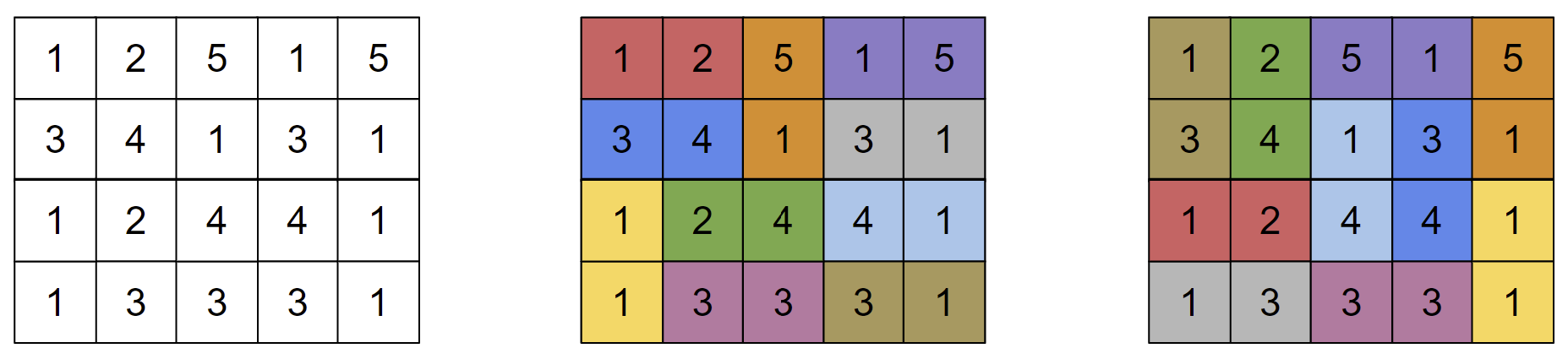
Поликарп и Монокарп помнят набор домино, с которого они начинали, но они потеряли таблицу $$$a$$$. Помогите им восстановить одну из возможных таблиц $$$a$$$, а также оба их решения, или определите, что такой таблицы не существует.
Первая строка содержит одно целое число $$$n$$$ ($$$1 \le n \le 3\cdot 10^5$$$).
В $$$i$$$-й из следующих $$$n$$$ строк содержится два целых числа $$$x_i$$$ и $$$y_i$$$ ($$$1 \le x_i, y_i \le 2n$$$).
Если решения нет, выведите одно целое число $$$-1$$$.
В противном случае выведите $$$m$$$ и $$$k$$$, высоту и ширину сетки головоломки, в первой строке вывода. Они должны удовлетворять условию $$$m\cdot k = 2n$$$.
В $$$i$$$-й из следующих $$$m$$$ строк должно быть $$$k$$$ целых чисел, $$$j$$$-е из которых $$$a_{ij}$$$.
Следующие $$$m$$$ строк описывают решение Поликарпа. Выведите $$$m$$$ строк по $$$k$$$ символов в каждой. Для каждой ячейки, если она покрыт верхней половиной домино в решении Поликарпа, в ней должна стоять буква «U». Аналогично, если она покрыта нижней, левой или правой половиной домино, она должна содержать «D», «L» или «R», соответственно.
Следующие $$$m$$$ строк должны описывать решение Монокарпа в том же формате, что и решение Поликарпа.
Если ответов несколько, выведите любой из них
1 1 2
-1
2 1 1 1 2
2 2 2 1 1 1 LR LR UU DD
10 1 3 1 1 2 1 3 4 1 5 1 5 3 1 2 4 3 3 4 1
4 5 1 2 5 1 5 3 4 1 3 1 1 2 4 4 1 1 3 3 3 1 LRULR LRDLR ULRLR DLRLR UULRU DDUUD LRDDU LRLRD
Дополнительные пустые строки добавляются в вывод для наглядности, но не являются обязательными.
Третий пример соответствует изображению из условия.
| Название |
|---|




