| Codeforces Round 805 (Div. 3) |
|---|
| Закончено |
Это сложная версия задачи. Единственное различие простой и сложной версии в количестве запросов.
Поликарп вырастил дерево из $$$n$$$ вершин. Напоминаем, что деревом из $$$n$$$ вершин называется неориентированный связный граф из $$$n$$$ вершин и $$$n-1$$$ ребра, не содержащий циклов.
Он называет множество вершин проходимым, если существует такой путь в дереве, который проходит через каждую вершину этого множества, не проходя по какому-либо ребру дважды. Путь может посещать другие вершины (не из этого множества).
Иными словами, множество вершин называется проходимым, если существует простой путь, который проходит по всем вершинам этого множества (и, возможно, каким-то другим).
Например для дерева ниже множества $$$\{3, 2, 5\}$$$, $$$\{1, 5, 4\}$$$, $$$\{1, 4\}$$$ проходимы, а $$$\{1, 3, 5\}$$$, $$$\{1, 2, 3, 4, 5\}$$$ — нет.
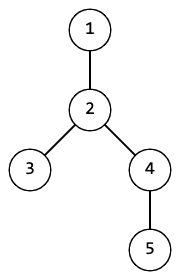
Поликарп просит вас ответить на $$$q$$$ запросов. Каждый запрос является множеством вершин. Для каждого запроса вам необходимо определить проходимо ли соответствующее множество вершин.
Первая строка входных данных содержит единственное целое число $$$n$$$ ($$$1 \le n \le 2 \cdot 10^5$$$) — количество вершин дерева.
Следующие $$$n - 1$$$ строк содержат описание дерева.
Каждая строка содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u, v \le n$$$, $$$u \ne v$$$) — индексы вершин, соединённых ребром.
Далее следует строка с единственным целым числом $$$q$$$ ($$$1 \le q \le 10^5$$$) — количество запросов.
Следующие $$$2 \cdot q$$$ строк содержат описания множеств.
Первая строка описания содержит целое число $$$k$$$ ($$$1 \le k \le n$$$) — размер множества.
Вторая строка описания содержит $$$k$$$ различных целых чисел $$$p_1, p_2, \dots, p_k$$$ ($$$1 \le p_i \le n$$$) — индексы вершин множества.
Гарантируется, что сумма значений $$$k$$$ по всем запросам не превосходит $$$2 \cdot 10^5$$$.
Выведите $$$q$$$ строк, каждая из которых содержит ответ на соответствующий запрос. В качестве ответа выведите «YES», если множество проходимо, и «NO» в противном случае.
Вы можете выводить ответ в любом регистре (например, строки «yEs», «yes», «Yes» и «YES» будут распознаны как положительный ответ).
5 1 2 2 3 2 4 4 5 5 3 3 2 5 5 1 2 3 4 5 2 1 4 3 1 3 5 3 1 5 4
YES NO YES NO YES
5 1 2 3 2 2 4 5 2 4 2 3 1 3 3 4 5 3 2 3 5 1 1
YES NO YES YES
| Название |
|---|




