| Codeforces Round 809 (Div. 2) |
|---|
| Закончено |
У вас есть последовательность из $$$n$$$ цветных блоков. Цвет $$$i$$$-го из них равен $$$c_i$$$. Цвета блоков являются целыми числами от $$$1$$$ до $$$n$$$.
Вы будете последовательно размещать блоки на бесконечной координатной сетке следующим образом:
- Сначала вы размещаете блок $$$1$$$ в клетке $$$(0, 0)$$$.
- Для $$$2 \le i \le n$$$ обозначим за $$$(x, y)$$$ клетку, в которой вы разместили $$$(i - 1)$$$-й блок. Вы можете разместить $$$i$$$-й блок в одну из свободных клеток $$$(x + 1, y)$$$, $$$(x - 1, y)$$$, $$$(x, y + 1)$$$ (но не в клетку $$$(x, y - 1)$$$). Обратите внимание, что вы не можете размещать блок в клетке, уже содержащей блок.
Башня состоит из $$$s$$$ блоков, расположенных в клетках $$$(x, y), (x, y + 1), \ldots, (x, y + s - 1)$$$ для некоторой клетки $$$(x, y)$$$ и целого числа $$$s$$$. Размер башни равен количеству блоков в ней $$$s$$$. Башня цвета $$$r$$$ это башня, состоящая только из блоков цвета $$$r$$$.
Для всех $$$r$$$ от $$$1$$$ до $$$n$$$ решите независимо следующую задачу:
- Вы хотите создать большую башню цвета $$$r$$$ в результате размещения всех блоков описанным выше образом. Чему равен максимальный размер такой башни?
В первой строке задано одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных. Далее следуют описания этих наборов.
В первой строке дано одно число $$$n$$$ ($$$1 \le n \le 10^5$$$) — длина последовательности блоков.
Во второй строке даны $$$n$$$ целых чисел $$$c_1, c_2, \ldots, c_n$$$ ($$$1 \le c_i \le n$$$) — цвета блоков.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите $$$n$$$ чисел. $$$r$$$-е из них должно быть равно максимальному размеру башни цвета $$$r$$$, которую Вы можете создать после размещения всех блоков. Если Вы не можете создать башню цвета $$$r$$$, то $$$r$$$-е число должно быть равно $$$0$$$.
671 2 3 1 2 3 164 2 2 2 4 41155 4 5 3 563 3 3 1 3 381 2 3 4 4 3 2 1
3 2 2 0 0 0 0 0 3 0 2 0 0 1 0 0 1 1 1 1 0 4 0 0 0 2 2 2 2 0 0 0 0
В первом наборе входных данных, один из способов создать башню цвета $$$1$$$ размера $$$3$$$ приведён ниже:
- разместить блок $$$1$$$ в клетке $$$(0, 0)$$$;
- разместить блок $$$2$$$ в клетке $$$(1, 0)$$$ (справа от блока $$$1$$$);
- разместить блок $$$3$$$ в клетке $$$(1, 1)$$$ (над блоком $$$2$$$);
- разместить блок $$$4$$$ в клетке $$$(0, 1)$$$ (слева от блока $$$3$$$);
- разместить блок $$$5$$$ в клетке $$$(-1, 1)$$$ (слева от блока $$$4$$$);
- разместить блок $$$6$$$ в клетке $$$(-1, 2)$$$ (над блоком $$$5$$$);
- разместить блок $$$7$$$ в клетке $$$(0, 2)$$$ (справа от блока $$$6$$$).
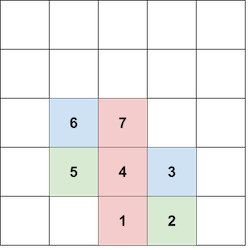
В клетках $$$(0, 0)$$$, $$$(0, 1)$$$ и $$$(0, 2)$$$ расположены блоки цвета $$$1$$$, образующие башню размера $$$3$$$.
Во втором наборе входных данных, обратите внимание, что следующее размещение блоков не является корректным, так как Вы не можете разместить блок $$$6$$$ ниже блока $$$5$$$:
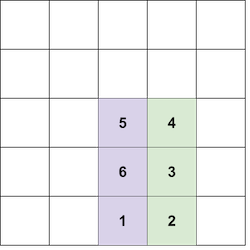
Можно показать, что невозможно создать башню цвета $$$4$$$ размера $$$3$$$.
| Название |
|---|




