| Codeforces Round 808 (Div. 1) |
|---|
| Закончено |
Вам дан связный неориентированный граф из $$$n$$$ вершин и $$$m$$$ рёбер. Вес $$$i$$$-го ребра равен $$$i$$$.
Ниже представлен некорректный алгоритм поиска минимального остовного дерева:
vis := массив длины n
s := множество рёбер
function dfs(u):
vis[u] := true
пройтись по каждому ребру (u, v) в порядке увеличения весов
if vis[v] = false
добавить ребро (u, v) в множество (s)
dfs(v)
function findMST(u):
установить все элементы (vis) в false
очистить множество (s)
dfs(u)
return множество (s)
Любой из вызовов функций findMST(1), findMST(2), ..., findMST(n) возвращает вам остовное дерево графа. Определите, какие из этих деревьев являются минимальными остовными деревьями.
Первая строка входных данных содержит два целых числа $$$n$$$, $$$m$$$ ($$$2\le n\le 10^5$$$, $$$n-1\le m\le 2\cdot 10^5$$$) — количество вершин и ребер в графе.
Каждая из следующих $$$m$$$ строк содержит два целых числа $$$u_i$$$ и $$$v_i$$$ ($$$1\le u_i, v_i\le n$$$, $$$u_i\ne v_i$$$), описывающих неориентированное ребро $$$(u_i,v_i)$$$ в графе, $$$i$$$-е ребро во входных данных имеет вес $$$i$$$.
Гарантируется, что граф связный и между любой парой вершин существует не более одного ребра.
Выведите строку $$$s$$$, состоящую из нулей и единиц, где $$$s_i=1$$$, если findMST(i) возвращает минимальное остовное дерево, и $$$s_i = 0$$$ иначе.
5 5 1 2 3 5 1 3 3 2 4 2
01111
10 11 1 2 2 5 3 4 4 2 8 1 4 5 10 5 9 5 8 2 5 7 4 6
0011111011
Ниже показан граф из первого примера:
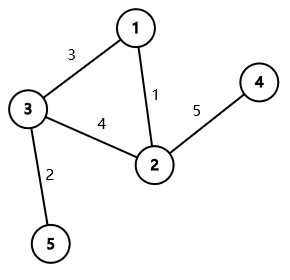
В этом графе существует только одно минимальное остовное дерево, состоящее из ребер $$$(1,2),(3,5),(1,3),(2,4)$$$, имеющих суммарный вес $$$1+2+3+5=11$$$.
Ниже описана часть вычислений при вызове findMST(1):
- реинициализируем массив vis и множество ребер s;
- вызываем dfs(1);
- vis[1] := true;
- итерируемся по ребрам $$$(1,2),(1,3)$$$;
- добавляем ребро $$$(1,2)$$$ во множество s, вызываем dfs(2):
- vis[2] := true;
- итерируемся по ребрам $$$(2,1),(2,3),(2,4)$$$;
- так как vis[1] = true, игнорируем ребро $$$(2,1)$$$;
- добавляем ребро $$$(2,3)$$$ во множество s, вызываем dfs(3):
- ...
В конце алгоритма будут выбраны ребра $$$(1,2),(2,3),(3,5),(2,4)$$$ с суммарным весом $$$1+4+2+5=12>11$$$, поэтому findMST(1) находит не минимальное остовное дерево.
Можно показать, что остальные остовные деревья являются минимальными, поэтому ответ 01111.
| Название |
|---|




