| Codeforces Round 810 (Div. 1) |
|---|
| Закончено |
У Родокса есть дерево из $$$n$$$ вершин, но он не помнит его структуру. Вершины дерева пронумерованы от $$$1$$$ до $$$n$$$.
Отрезок $$$[l,r]$$$ ($$$1 \leq l \leq r \leq n$$$) называется хорошим, если вершины $$$l$$$, $$$l + 1$$$, ..., $$$r$$$ образуют связную компоненту в дереве Родокса. Иначе отрезок называется плохим.
Например, для дерева на рисунке ниже только отрезок $$$[3,4]$$$ является плохим, а все остальные отрезки хорошие.
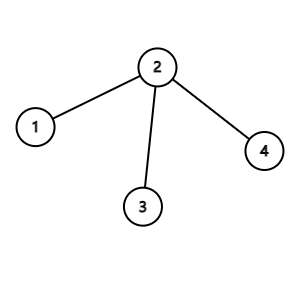
Для каждого из $$$\frac{n(n+1)}{2}$$$ отрезков Родокс помнит, хорошим является этот отрезок, или плохим. Можете помочь ему восстановить дерево? Если существуют несколько решений, выведите любое из них.
Гарантируется, что существует хотя бы одно дерево, подходящее под описание Родокса.
Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \leq t \leq 1000$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит целое число $$$n$$$ ($$$1 \leq n \leq 2000$$$) — количество вершин.
Далее следуют $$$n$$$ строк. $$$i$$$-я из этих строк содержит строку $$$good_i$$$ длины $$$n+1-i$$$, состоящую из цифр 0 и 1. Если отрезок $$$[i,i+j-1]$$$ является хорошим, то $$$j$$$-й символ строки $$$good_i$$$ равен 1, иначе $$$j$$$-й символ строки $$$good_i$$$ равен 0.
Гарантируется, что существует хотя бы одно дерево, подходящее под данное описание. .
Гарантируется, что сумма значений $$$n$$$ по всем наборам входных данных не превосходит $$$2000$$$.
Для каждого набора входных данных выведите $$$n-1$$$ строку, описывающую ваше дерево.
В $$$i$$$-й из этих строк выведите два целых числа $$$u_i$$$ и $$$v_i$$$ ($$$1 \leq u_i,v_i \leq n$$$), означающие, что в дереве есть ребро между вершинами $$$u_i$$$ и $$$v_i$$$.
Если существуют несколько решений, выведите любое из них.
341111111101611111111111111111111112100100000001111000000011000000000100000000100100011110000100000100001001111101
1 2 2 3 2 4 1 2 2 3 3 4 4 5 5 6 2 3 6 7 10 11 2 4 6 8 10 12 1 4 5 8 9 12 5 12 2 12
Первый пример объяснен в условии.
Во втором примере одно из возможных деревьев следующее:
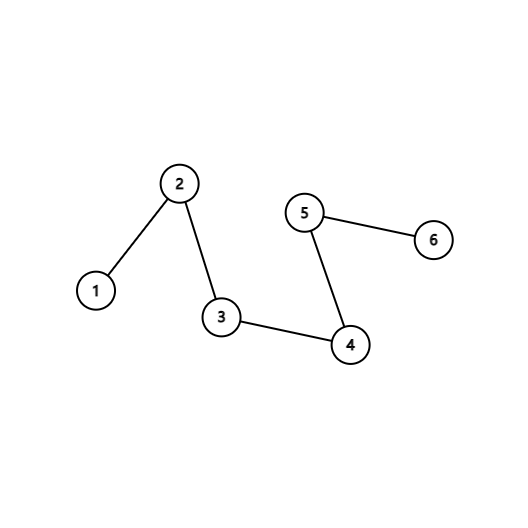
В третьем примере одно из возможных деревьев следующее:
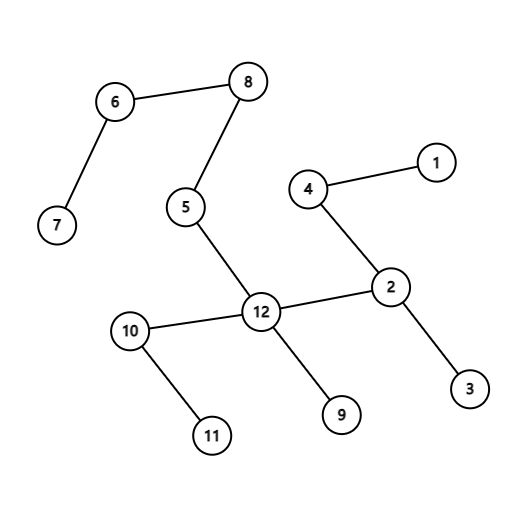
| Название |
|---|




