| Codeforces Round 813 (Div. 2) |
|---|
| Закончено |
Дерево — это неориентированный связный граф без циклов. Взвешенное дерево — это дерево, каждому ребру которого назначен некоторый вес. Степень вершины — это количество ребер, прилегающих к данной вершине.
Вам дано взвешенное дерево с $$$n$$$ вершинами, каждое ребро которого имеет вес $$$1$$$. Определим множество вершин $$$L$$$ следующим образом: все вершины, степень которых равна $$$1$$$, входят в это множество, остальные вершины в это множество не входят.
Вам необходимо ответить на $$$q$$$ независимых запросов. В $$$i$$$-м запросе:
- Вам дано целое положительное число $$$x_i$$$.
- Для всех $$$u,v \in L$$$ таких, что $$$u < v$$$, добавьте ребро $$$(u, v)$$$ с весом $$$x_i$$$ в граф (который изначально является данным вам деревом).
- Найдите диаметр итогового графа.
Диаметр графа равен $$$\max\limits_{1 \le u < v \le n}{\operatorname{d}(u, v)}$$$, где $$$\operatorname{d}(u, v)$$$ — это длина кратчайшего пути между вершинами $$$u$$$ и $$$v$$$.
В первой строке находится единственное целое число $$$n$$$ ($$$3 \le n \le 10^6$$$).
Во второй строке находится $$$n - 1$$$ целое число $$$p_2,p_3,\ldots,p_n$$$ ($$$1 \le p_i < i$$$), каждое из которых означает, что в графе есть ребро между вершинами $$$i$$$ и $$$p_i$$$. Гарантируется, что данные ребра образуют дерево.
В третьей строке находится единственное целое число $$$q$$$ ($$$1 \le q \le 10$$$).
В четвертой строке находится $$$q$$$ целых чисел $$$x_1,x_2,\ldots,x_q$$$ ($$$1 \le x_i \le n$$$). Все $$$x_i$$$ попарно различны.
В единственной строке выведите $$$q$$$ целых чисел, которые являются ответами на запросы.
4 1 2 2 4 1 2 3 4
1 2 2 2
7 1 2 3 4 2 1 7 2 1 3 7 5 6 4
3 3 4 5 5 5 4
3 1 2 1 1
1
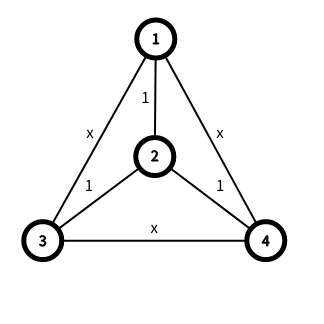
Граф в первом тесте после добавления ребер:
| Название |
|---|




