| Codeforces Round 812 (Div. 2) |
|---|
| Закончено |
Вы живете на бесконечной плоскости с введенными декартовыми координатами. За один шаг вы можете пойти в одну из четырех соседних точек (налево, направо, наверх или вниз).
Более формально, если вы стоите в точке $$$(x, y)$$$, вы можете:
- пойти налево и переместиться в точку $$$(x - 1, y)$$$, или
- пойти направо и переместиться в точку $$$(x + 1, y)$$$, или
- пойти наверх и переместиться в точку $$$(x, y + 1)$$$, или
- пойти вниз и переместиться в точку $$$(x, y - 1)$$$.
На плоскости расположены $$$n$$$ коробок. $$$i$$$-я из этих коробок находится в точке с координатами $$$(x_i,y_i)$$$. Гарантируется, что коробки находятся либо на оси $$$x$$$, либо на оси $$$y$$$, то есть $$$x_i=0$$$, или $$$y_i=0$$$.
Вы можете подобрать коробку если находитесь в одной точке с ней. Найдите минимальное число шагов, необходимое, чтобы собрать все коробки, при условии что вы начинаете и заканчиваете в точке $$$(0,0)$$$.
В первой строке содержится одно целое число $$$t$$$ ($$$1 \le t \le 100$$$) — количество наборов входных данных.
Вторая строка каждого набора содержит одно целое число $$$n$$$ ($$$1 \le n \le 100$$$) — количество коробок.
$$$i$$$-я из следующих $$$n$$$ строк содержит два целых числа $$$x_i$$$ и $$$y_i$$$ ($$$-100 \le x_i, y_i \le 100$$$) — координаты $$$i$$$-й коробки. Гарантируется, что или $$$x_i=0$$$, или $$$y_i=0$$$.
Обратите внимание, что сумма значений $$$n$$$ по всем наборам входных данных не ограничена.
Для каждого набора входных данных выведите одно число — минимальное необходимое число шагов.
340 -21 0-1 00 230 2-3 00 -110 0
12 12 0
В первом примере одна из оптимальных последовательностей шагов показана ниже.
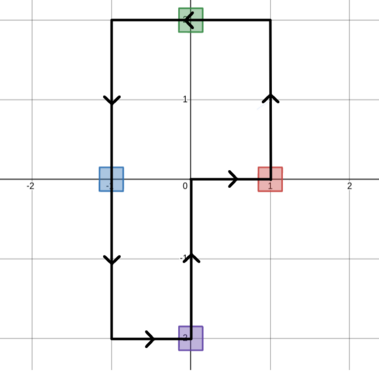 $$$$$$(0,0) \to (1,0) \to (1,1) \to (1, 2) \to (0,2) \to (-1,2) \to (-1,1) \to (-1,0) \to (-1,-1) \to (-1,-2) \to (0,-2) \to (0,-1) \to (0,0)$$$$$$
$$$$$$(0,0) \to (1,0) \to (1,1) \to (1, 2) \to (0,2) \to (-1,2) \to (-1,1) \to (-1,0) \to (-1,-1) \to (-1,-2) \to (0,-2) \to (0,-1) \to (0,0)$$$$$$ Во втором примере одна из оптимальных последовательностей шагов показана на рисунке ниже.
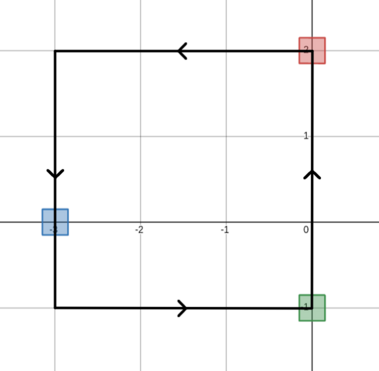 $$$$$$(0,0) \to (0,1) \to (0,2) \to (-1, 2) \to (-2,2) \to (-3,2) \to (-3,1) \to (-3,0) \to (-3,-1) \to (-2,-1) \to (-1,-1) \to (0,-1) \to (0,0)$$$$$$
$$$$$$(0,0) \to (0,1) \to (0,2) \to (-1, 2) \to (-2,2) \to (-3,2) \to (-3,1) \to (-3,0) \to (-3,-1) \to (-2,-1) \to (-1,-1) \to (0,-1) \to (0,0)$$$$$$ В третьем примере можно собрать все коробки не делая шагов.
| Название |
|---|




