| Codeforces Round 816 (Div. 2) |
|---|
| Finished |
Stanley and Megan decided to shop in the "Crossmarket" grocery store, which can be represented as a matrix with $$$n$$$ rows and $$$m$$$ columns.
Stanley and Megan can move to an adjacent cell using $$$1$$$ unit of power. Two cells are considered adjacent if they share an edge. To speed up the shopping process, Megan brought her portals with her, and she leaves one in each cell she visits (if there is no portal yet). If a person (Stanley or Megan) is in a cell with a portal, that person can use $$$1$$$ unit of power to teleport to any other cell with a portal, including Megan's starting cell.
They decided to split up: Stanley will go from the upper-left cell (cell with coordinates $$$(1, 1)$$$) to the lower-right cell (cell with coordinates $$$(n, m)$$$), whilst Megan needs to get from the lower-left cell (cell with coordinates $$$(n, 1)$$$) to the upper-right cell (cell with coordinates $$$(1, m)$$$).
What is the minimum total energy needed for them both to do that?
Note that they can choose the time they move. Time does not affect energy.
Each test contains multiple test cases. The first line contains the number of test cases $$$t$$$ ($$$1 \le t \le 1000$$$). Description of the test cases follows.
The only line in the test case contains two integers $$$n$$$ and $$$m$$$ ($$$1 \le n, m \le 10^5$$$).
For each test case print a single integer on a new line – the answer.
77 55 71 1100000 10000057 2281 55 1
15 15 0 299998 340 5 5
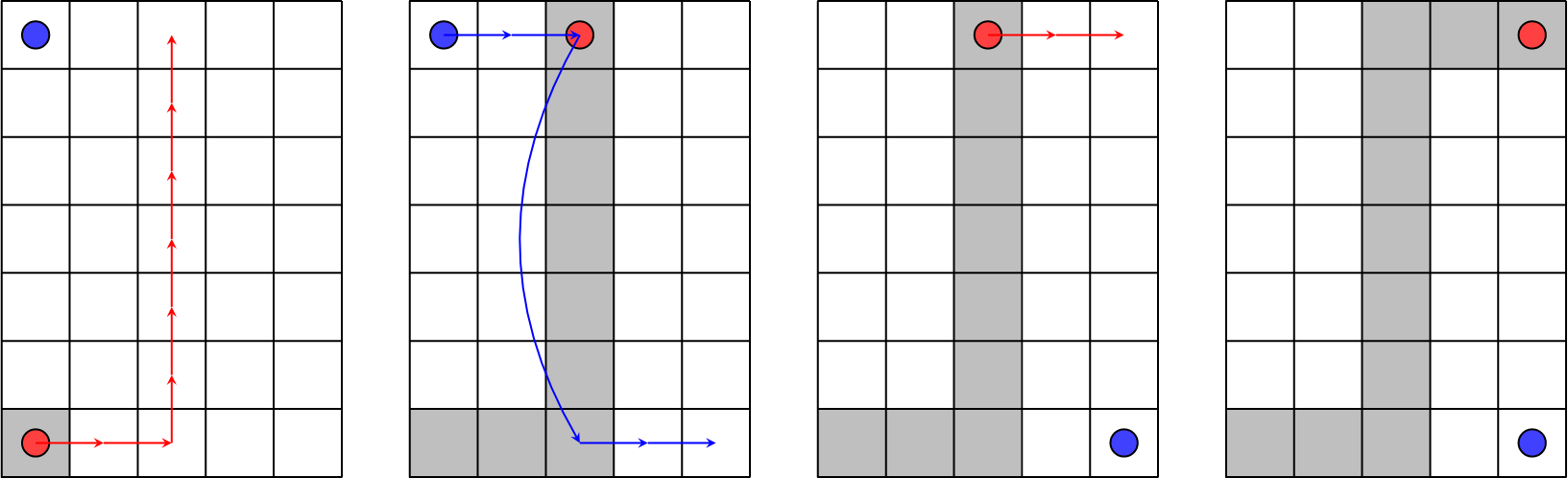
In the first test case they can stick to the following plan:
- Megan (red circle) moves to the cell $$$(7, 3)$$$. Then she goes to the cell $$$(1, 3)$$$, and Stanley (blue circle) does the same.
- Stanley uses the portal in that cell (cells with portals are grey) to get to the cell $$$(7, 3)$$$. Then he moves to his destination — cell $$$(7, 5)$$$.
- Megan also finishes her route and goes to the cell $$$(1, 5)$$$.
The total energy spent is $$$(2 + 6) + (2 + 1 + 2) + (2)= 15$$$, which is our final answer.
| Name |
|---|




