Недавно Поликарп заинтересовался последовательностями псевдослучайных чисел. Он узнал, что во многих языках программирования такие последовательности генерируются одинаковым образом: 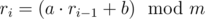 (для i ≥ 1). Здесь a, b, m — константы, фиксированные для данной реализации генератора псевдослучайных чисел, r0 — так называемый randseed (это значение может быть установлено из программы с помощью функций вроде RandSeed(r) или srand(n)), а
(для i ≥ 1). Здесь a, b, m — константы, фиксированные для данной реализации генератора псевдослучайных чисел, r0 — так называемый randseed (это значение может быть установлено из программы с помощью функций вроде RandSeed(r) или srand(n)), а 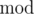 обозначает операцию взятия остатка от деления.
обозначает операцию взятия остатка от деления.
Например, если a = 2, b = 6, m = 12, r0 = 11, то генерируемая последовательность будет иметь вид: 4, 2, 10, 2, 10, 2, 10, 2, 10, 2, 10, ....
Поликарп понял, что любая такая последовательность рано или поздно зациклится, но цикл может встретиться не сразу, то есть существует предпериод и период. В примере выше длина предпериода равна 1, а периода — 2.
Ваша задача — найти период такой последовательности по заданным a, b, m и r0. Формально, необходимо найти минимальное натуральное t, для которого существует такое натуральное k, что для любого i ≥ k: ri = ri + t.
В единственной строке входных данных записаны через пробел четыре целых числа a, b, m и r0 (1 ≤ m ≤ 105, 0 ≤ a, b ≤ 1000, 0 ≤ r0 < m).
Выведите единственное целое число — искомый период последовательности.
2 6 12 11
2
2 3 5 1
4
3 6 81 9
1
Первый пример разобран выше.
Во втором примере последовательность имеет вид (начиная с первого элемента): 0, 3, 4, 1, 0, 3, 4, 1, 0, ...
В третьем примере последовательность имеет вид (начиная с первого элемента): 33, 24, 78, 78, 78, 78, ...
| Название |
|---|




