Прошлым летом Feluda подарил Lalmohan-Babu правильную скобочную последовательность $$$s$$$ длины $$$2 n$$$.
Topshe скучал во время летних каникул, и поэтому решил нарисовать неориентированный граф из $$$2 n$$$ вершин, используя правильную скобочную последовательность $$$s$$$. Для каждых двух различных вершин $$$i$$$ и $$$j$$$ ($$$1 \le i < j \le 2 n$$$) Topshe рисует ребро между этими двумя вершинами тогда и только тогда, когда подотрезок $$$s[i \ldots j]$$$ образует правильную скобочную последовательность.
Определите количество компонент связности в графе Topshe.
Смотрите определения подчёркнутых терминов в Примечании.
Каждый тест состоит из нескольких наборов входных данных. Первая строка содержит единственное целое число $$$t$$$ ($$$1 \le t \le 10^5$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит единственное целое число $$$n$$$ ($$$1 \le n \le 10^5$$$) — количество открывающих скобок в строке $$$s$$$.
Вторая строка каждого набора входных данных содержит строку $$$s$$$ длины $$$2 n$$$ — правильная скобочная последовательность, состоящая из $$$n$$$ открывающих скобок «(» и $$$n$$$ закрывающих скобок «)».
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$10^5$$$.
Для каждого набора входных данных выведите единственное целое число — количество компонент связности в графе Topshe.
41()3()(())3((()))4(())(())
1 2 3 3
Объяснение примера:
В первом наборе входных данных, граф, построенный из скобочной последовательности (), является просто графом, содержащим вершины $$$1$$$ и $$$2$$$, соединёнными единственным ребром.
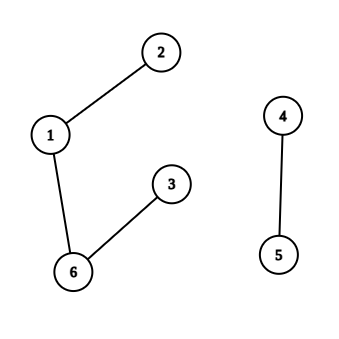
Во втором наборе входных данных, граф, построенный из скобочной последовательности ()(()) будет следующим (содержит две компоненты связности):
Определения подчёркнутых терминов:
- Последовательность скобок является правильной, если её можно превратить в корректное математическое выражение путём добавления символов $$$+$$$ и $$$1$$$. Например, последовательности (())(), () и (()(())) являются правильными, а )(, (() и (()))( не являются.
- Подотрезок $$$s[l \ldots r]$$$ обозначает последовательность $$$[s_l, s_{l + 1}, \ldots, s_r]$$$.
- Компонента связности является множеством вершин $$$X$$$ таким, что для каждых двух вершин из этого множества существует хотя бы один путь в графе, соединяющий эти вершины, но добавление любой другой вершины в $$$X$$$ нарушает это правило.
| Название |
|---|




