Вам дан связный, неориентированный и невзвешенный граф с $$$n$$$ вершинами и $$$m$$$ рёбрами. Обратите внимание на ограничение на количество рёбер: $$$m \le n + 2$$$.
Давайте скажем, что мы красим некоторые рёбра в красный и оставшиеся рёбра в синий. Теперь рассмотрим только красные рёбра и посчитаем количество компонент связности в графе. Пусть это значение равно $$$c_1$$$. Аналогично, рассмотрим только синие рёбра и посчитаем количество компонент связности в графе. Пусть это значение равно $$$c_2$$$.
Найдите распределение цветов по рёбрам такое, что величина $$$c_1+c_2$$$ минимальна.
Каждый тест состоит из нескольких наборов входных данных. Первая строка содержит единственное целое число $$$t$$$ ($$$1 \le t \le 10^5$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит два целых числа $$$n$$$ и $$$m$$$ ($$$2 \le n \le 2 \cdot 10^5$$$; $$$n-1 \leq m \leq \min{\left(n+2,\frac{n \cdot (n-1)}{2}\right)}$$$) — количество вершин и рёбер в графе соответственно.
Затем следуют $$$m$$$ строк. $$$i$$$-я строка содержит два целых числа $$$u_i$$$ и $$$v_i$$$ ($$$1 \le u_i,v_i \le n$$$, $$$u_i \ne v_i$$$) обозначающая, что $$$i$$$-е ребро соединяет вершины $$$u_i$$$ и $$$v_i$$$. Гарантируется, что в графе нет петель и кратных рёбер. Также гарантируется, что граф связен.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$10^6$$$. Гарантируется, что сумма $$$m$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^6$$$.
Для каждого набора входных данных выведите бинарную строку длины $$$m$$$. $$$i$$$-й символ строки должен быть 1, если $$$i$$$-е ребро должно иметь красный цвет, и 0, если оно должно иметь синий цвет. Если существует несколько способов распределить цвета, чтобы получить минимальную величину, вы можете вывести любой.
45 71 22 33 44 55 11 33 54 41 22 31 43 46 71 21 33 44 51 45 66 22 11 2
0111010 1001 0001111 0
- Граф в первом наборе входных данных следующий:
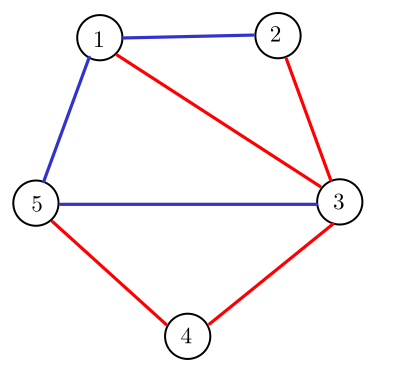
$$$c_1 + c_2 = 1 + 2 = 3$$$
- Граф во втором наборе входных данных следующий:
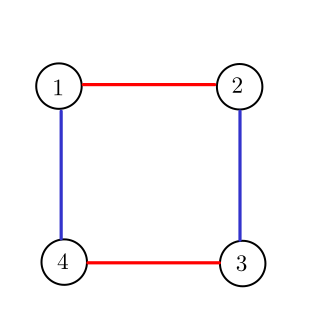
$$$c_1 + c_2 = 2 + 2 = 4$$$
| Название |
|---|




