| Codeforces Round 824 (Div. 2) |
|---|
| Закончено |
Есть $$$n$$$ кусочков от шкурки мандарина, $$$i$$$-й из них имеет некоторый размер $$$a_i$$$. За одно действие можно любой кусок размера $$$x$$$ порвать на два кусочка с положительными целочисленными размерами $$$y$$$ и $$$z$$$ такими, что $$$y + z = x$$$.
Хочется, чтобы размеры любых двух кусочков отличались строго меньше чем в два раза. Другими словами, не должно быть двух кусочков размеров $$$x$$$ и $$$y$$$ таких, что $$$2x \le y$$$. Какого минимального количества действий достаточно для выполнения этого условия?
Первая строка входных данных содержит единственное целое число $$$t$$$ ($$$1 \le t \le 100$$$) — количество наборов входных данных. Описание наборов входных данных следует ниже.
Первая строка каждого набора содержит одно целое число $$$n$$$ ($$$1 \le n \le 100$$$).
Затем следует одна строка, в которой содержится $$$n$$$ целых чисел $$$a_1 \le a_2 \le \ldots \le a_n$$$ ($$$1 \le a_i \le 10^7$$$).
Для каждого набора входных данных выведите одну строку, содержащую минимальное количество действий.
351 2 3 4 5110335600 900 1300 2000 2550
10 0 4
В первом наборе входных данных у нас изначально имеется кусочек размера $$$1$$$, поэтому в конце все кусочки должны иметь именно размер $$$1$$$. Итоговое количество действий: $$$0 + 1 + 2 + 3 + 4 = 10$$$.
Во втором наборе у нас всего один кусок, поэтому ничего делать не требуется и ответ: $$$0$$$ действий.
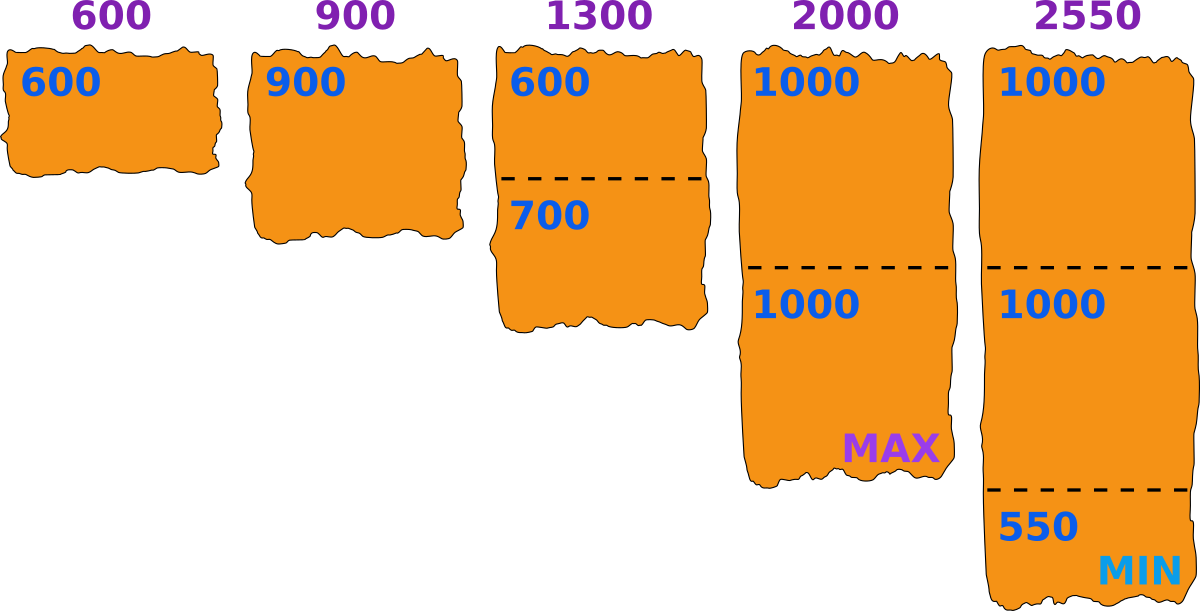
В третьем наборе один из возможных вариантов разрезов: $$$600,\ 900,\ (600 | 700),\ (1000 | 1000),\ (1000 | 1000 | 550)$$$. Этот вариант можно увидеть на изображении ниже. Максимальный кусок имеет размер $$$1000$$$ и менее чем в $$$2$$$ раза превосходит минимальный размером $$$550$$$. Произведено $$$4$$$ действия, можно показать, что это минимальное количество действий.
| Название |
|---|




