| Codeforces Round 831 (Div. 1 + Div. 2) |
|---|
| Закончено |
Для корневого дерева определим значение вершины $$$u$$$ в дереве рекурсивно как MEX$$$^\dagger$$$ значений её детей. Обратите внимание, что это только дети, а не все её потомки. В частности, значение листа равно $$$0$$$.
У Пака Чанека есть корневое дерево, которое изначально содержит только одну вершину с индексом $$$1$$$, являющуюся корнем. Пак Чанек будет исполнять $$$q$$$ запросов. В $$$i$$$-м запросе Паку Чанеку задано целое число $$$x_i$$$. Паку Чанеку нужно добавить новую вершину с индексом $$$i+1$$$ в качестве ребенка вершины $$$x_i$$$. После добавления новой вершины Пак Чанек должен пересчитать значения всех вершин и сообщить сумму значений всех вершин в текущем дереве.
$$$^\dagger$$$ MEX (minimum excluded) массива это наименьшее неотрицательное целое число, которого нет в массиве. Например, MEX массива $$$[0,1,1,2,6,7]$$$ равен $$$3$$$, а MEX $$$[6,9]$$$ равен $$$0$$$.
Первая строка входных данных содержит целое число $$$q$$$ ($$$1 \le q \le 3 \cdot 10^5$$$) — количество запросов.
Каждая из следующих $$$q$$$ строк содержит целое число $$$x_i$$$ ($$$1 \leq x_i \leq i$$$) — описание $$$i$$$-го запроса.
Для каждого запроса выведите строку, содержащую целое число — сумму новых значений всех вершин в дереве после добавления вершины.
7 1 1 3 2 5 2 1
1 1 3 2 4 4 7
8 1 1 1 1 5 6 7 8
1 1 1 1 3 2 4 3
В первом примере после $$$6$$$-го запроса дерево примет следующий вид.
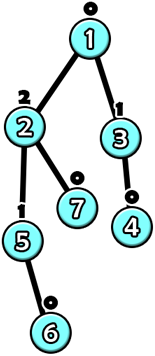
- Вершина $$$7$$$ — лист, поэтому её значение равно $$$0$$$.
- Вершина $$$6$$$ — лист, поэтому её значение равно $$$0$$$.
- Вершина $$$5$$$ имеет единственного ребенка со значением $$$0$$$, поэтому её значение равно $$$1$$$.
- Вершина $$$4$$$ — лист, поэтому её значение равно $$$0$$$.
- Вершина $$$3$$$ имеет единственного ребенка со значением $$$0$$$, поэтому её значение равно $$$1$$$.
- Вершина $$$2$$$ имеет детей со значениями $$$0$$$ и $$$1$$$, поэтому её значение равно $$$2$$$.
- Вершина $$$1$$$ имеет детей со значениями $$$1$$$ и $$$2$$$, поэтому её значение равно $$$0$$$.
Сумма значений всех вершин равна $$$0+0+1+0+1+2+0=4$$$.
| Название |
|---|




