Вам задано дерево, состоящее из $$$n$$$ вершин. Первоначально в каждой вершине записано число $$$0$$$.
Вам нужно обработать $$$m$$$ запросов двух видов:
- Вам задан номер вершины $$$v$$$. Выведите значение в данной вершине $$$v$$$.
- Вам заданы номера вершин $$$u$$$ и $$$v$$$, и значения $$$k$$$ и $$$d$$$ ($$$d \le 20$$$). Вам нужно прибавить $$$k$$$ к значению каждой вершины, расстояние от которой до пути из $$$u$$$ в $$$v$$$ не превосходит $$$d$$$.
Расстояние между двумя вершинами $$$x$$$ и $$$y$$$ равно количеству ребер на пути из $$$x$$$ в $$$y$$$. Например, расстояние от $$$x$$$ до самой $$$x$$$ равно $$$0$$$.
Расстояние от вершины $$$v$$$ до некоторого пути из $$$x$$$ в $$$y$$$ равно минимуму из расстояний от $$$v$$$ до любой вершины на пути из $$$x$$$ в $$$y$$$.
В первой строке задано одно целое число $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$) — количество вершин в дереве.
В следующих $$$n - 1$$$ строках заданы ребра дерева — по одному в строке. В каждой строке заданы два целых числа $$$u$$$ и $$$v$$$ ($$$1 \le u, v \le n$$$; $$$u \neq v$$$) — соответствующее ребро дерева. Гарантируется, что заданные ребра образуют дерево.
В следующей строке задано одно целое число $$$m$$$ ($$$1 \le m \le 2 \cdot 10^5$$$) — количество запросов.
В следующих $$$m$$$ строках заданы сами запросы — по одному в строке. Каждый запрос имеет один из следующих типов:
- $$$1$$$ $$$v$$$ ($$$1 \le v \le n$$$) — запрос первого типа;
- $$$2$$$ $$$u$$$ $$$v$$$ $$$k$$$ $$$d$$$ ($$$1 \le u, v \le n$$$; $$$1 \le k \le 1000$$$; $$$0 \le d \le 20$$$) — запрос второго типа.
Дополнительное ограничение на входные данные: среди запросов есть хотя бы один запрос первого типа.
Для каждого запроса первого типа выведите текущее значение в заданной вершине.
6 1 2 1 3 4 2 5 2 3 6 14 2 4 5 10 2 1 3 1 6 2 1 1 10 20 2 6 6 10 20 1 3 2 3 2 10 0 2 5 2 10 1 1 1 1 2 1 3 1 4 1 5 1 6
10 0 30 50 50 40 40 40 20
Дерево из первого примера:
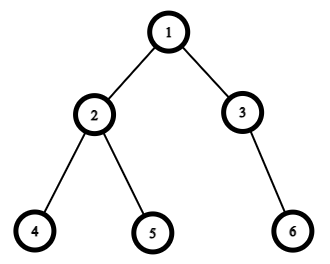
- «$$$2$$$ $$$4$$$ $$$5$$$ $$$10$$$ $$$2$$$»: попадающие под прибавление вершины — это $$$\{4, 2, 5, 1, 3\}$$$;
- «$$$2$$$ $$$1$$$ $$$1$$$ $$$10$$$ $$$20$$$» и «$$$2$$$ $$$6$$$ $$$6$$$ $$$10$$$ $$$20$$$»: все вершины попадают под прибавление, так как расстояние до $$$1$$$ ($$$6$$$) меньше $$$20$$$ у любой вершины;
- «$$$2$$$ $$$3$$$ $$$2$$$ $$$10$$$ $$$0$$$»: попадающие под прибавление вершины — это $$$\{3, 1, 2\}$$$;
- «$$$2$$$ $$$5$$$ $$$2$$$ $$$10$$$ $$$1$$$»: попадающие под прибавление вершины — это $$$\{5, 2, 4, 1\}$$$.
| Название |
|---|




