| Codeforces Global Round 24 |
|---|
| Закончено |
У Дореми $$$n$$$ ведерок с краской, они могут быть представлены в виде массива $$$a$$$ длины $$$n$$$. Ведерко $$$i$$$ содержит краску цвета $$$a_i$$$. Изначально $$$a_i=i$$$.
У Дореми есть $$$m$$$ отрезков $$$[l_i,r_i]$$$ ($$$1 \le l_i \le r_i \le n$$$). Каждый отрезок описывает одну операцию. $$$i$$$-я операция выполняется следующим образом:
- Для всех $$$j$$$ таких, что $$$l_i < j \leq r_i$$$, присвоить $$$a_j := a_{l_i}$$$.
Кроме этого у Дореми есть целое число $$$k$$$. Для каждого целого числа $$$x$$$ от $$$0$$$ до $$$m-1$$$ Дореми хочет знать, сколько различных цветов будет в массиве красок, если выполнить операции $$$x \bmod m +1, (x+1) \bmod m + 1, \ldots, (x+k-1) \bmod m +1$$$. Можете ей помочь вычислить эти значения? Обратите внимание, для каждого $$$x$$$ отдельно мы начинаем с изначального массива и выполняем только данные $$$k$$$ операций в данном порядке.
Первая строка содержит три целых числа $$$n$$$, $$$m$$$ и $$$k$$$ ($$$1\le n,m\le 2\cdot 10^5$$$, $$$1 \le k \le m$$$) — длину массива $$$a$$$, количество операций, а также число, которое есть у Дореми.
В $$$i$$$-й из следующих $$$m$$$ строк содержатся два целых числа $$$l_i$$$ и $$$r_i$$$ ($$$1\le l_i\le r_i\le n$$$) — границы $$$i$$$-го отрезка.
Выведите $$$m$$$ целых чисел. $$$(x+1)$$$-е из этих чисел должно быть равно итоговому количеству различных цветов, если к изначальному массиву применить операции $$$x \bmod m +1, (x+1) \bmod m + 1, \ldots, (x+k-1) \bmod m +1$$$.
7 5 5 3 5 2 3 4 6 5 7 1 2
3 3 3 3 2
10 9 4 1 1 2 3 3 4 7 9 6 8 5 7 2 4 9 10 1 3
6 6 7 6 5 5 7 7 7
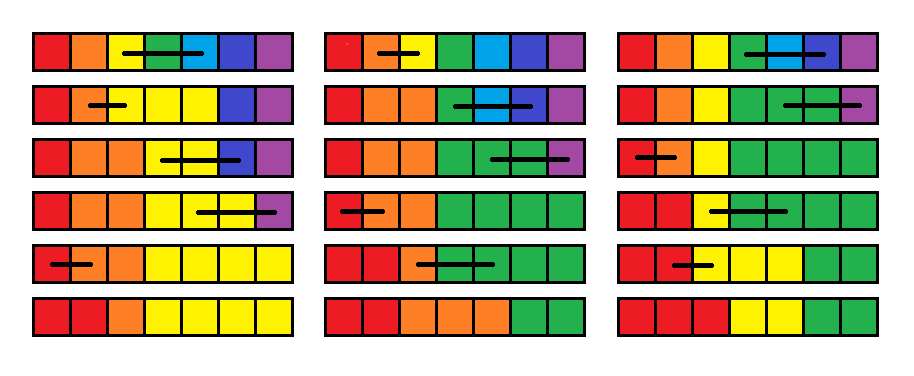
Рисунок ниже показывает массив, получающийся при значениях $$$x=0,1,2$$$, соответственно.
| Название |
|---|




