| Codeforces Round 837 (Div. 2) |
|---|
| Закончено |
У Хоссама есть невзвешенное дерево $$$G$$$, в вершинах которого записаны буквы.
Через $$$s(v, \, u)$$$ Хоссам обозначает строку, которая получается при написании всех букв на единственном простом пути из вершины $$$v$$$ в вершину $$$u$$$ в дереве $$$G$$$.
Строка $$$a$$$ является подпоследовательностью строки $$$s$$$, если $$$a$$$ может быть получена из $$$s$$$ путем удаления нескольких символов (возможно, ни одного). Например, «dores», «cf» и «for» являются подпоследовательностями «codeforces», а «decor» и «fork» не являются.
Палиндромом называется строка, читающаяся одинаково слева направо и справа налево. Например, «abacaba» — палиндром, а «abac» — нет.
Под-палиндромом строки $$$s$$$ Хоссам называет подпоследовательность $$$s$$$, являющуюся палиндромом. Например, «k», «abba» и «abhba» являются под-палиндромом строки «abhbka», а «abka» и «cat» — нет.
Максимальным под-палиндромом строки $$$s$$$ Хоссам называет под-палиндром $$$s$$$, имеющий максимальную длину среди всех под-палиндромов $$$s$$$. Например, у строки «abhbka» есть только один максимальный под-палиндром — «abhba». Но может быть и так, что у строки несколько максимальных под-палиндромов: у строки «abcd» целых $$$4$$$ максимальных под-палиндрома.
Хоссам просит вас найти длину самого длинного максимального под-палиндрома среди всех $$$s(v, \, u)$$$ в заданном дереве $$$G$$$.
Еще раз обращаем Ваше внимание на то, что под-палиндром — это подпоследовательность, а не подстрока.
В первой строке входного файла задано одно целое число $$$t$$$ ($$$1 \le t \le 200$$$) — количество наборов входных данных.
В первой строке каждого набора входных данных задано одно целое число $$$n$$$ ($$$1 \le n \le 2 \cdot 10^3$$$) — количество вершин в дереве.
Во второй строке задана строка $$$s$$$ длины $$$n$$$, $$$i$$$-й символ которой задает букву, которая записана в вершине дерева с номером $$$i$$$. Гарантируется, что все символы этой строке — маленькие буквы латинского алфавита.
Далее идут $$$n - 1$$$ строк, описывающие ребра в дереве. Каждое ребро задаётся двумя целыми числами $$$v$$$ и $$$u$$$ ($$$1 \le v, \, u \le n$$$, $$$v \neq u$$$). Эти два числа означают, что в дереве есть ребро $$$(v, \, u)$$$. Гарантируется, что заданные ребра образуют дерево.
Гарантируется, что сумма по всем $$$n$$$ не превышает $$$2 \cdot 10^3$$$.
Для каждого набора входных данных выведите одно число — длину самого длинного максимального под-палиндрома среди всех $$$s(v, \, u)$$$.
25abaca1 21 33 44 59caabadedb1 22 32 41 55 65 75 88 9
3 5
В первом примере искомым подпалиндромом может быть «aaa», символы которого расположены в вершинах $$$1, \, 3, \, 5$$$ или «aca», символы которого расположены в вершинах $$$1, \, 4, \, 5$$$.
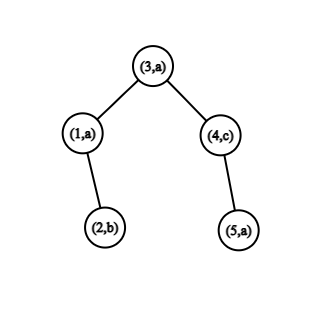 Дерево из первого примера.
Дерево из первого примера. Во втором примере единственным искомым палиндромом является «bacab», символы которого расположены в вершинах $$$4, \, 2, \, 1, \, 5, \, 9$$$.
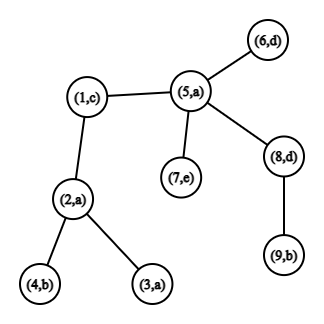 Дерево из второго примера.
Дерево из второго примера.
| Название |
|---|




