| Codeforces Round 848 (Div. 2) |
|---|
| Finished |
Recently, a tree has fallen on Bob's head from the sky. The tree has $$$n$$$ nodes. Each node $$$u$$$ of the tree has an integer number $$$a_u$$$ written on it. But the tree has no fixed root, as it has fallen from the sky.
Bob is currently studying the tree. To add some twist, Alice proposes a game. First, Bob chooses some node $$$r$$$ to be the root of the tree. After that, Alice chooses a node $$$v$$$ and tells him. Bob then can pick one or more nodes from the subtree of $$$v$$$. His score will be the bitwise XOR of all the values written on the nodes picked by him. Bob has to find the maximum score he can achieve for the given $$$r$$$ and $$$v$$$.
As Bob is not a good problem-solver, he asks you to help him find the answer. Can you help him? You need to find the answers for several combinations of $$$r$$$ and $$$v$$$ for the same tree.
Recall that a tree is a connected undirected graph without cycles. The subtree of a node $$$u$$$ is the set of all nodes $$$y$$$ such that the simple path from $$$y$$$ to the root passes through $$$u$$$. Note that $$$u$$$ is in the subtree of $$$u$$$.
Each test contains multiple test cases. The first line contains the number of test cases $$$t$$$ ($$$1 \le t \le 10^5$$$). The description of the test cases follows.
The first line contains an integer $$$n$$$ ($$$2\leq n\leq 2 \cdot 10^5$$$) — the number of nodes of the tree.
The next line contains $$$n$$$ space-separated integers $$$a_1, a_2, \dots, a_n$$$ ($$$1\leq a_i\leq 10^9$$$) — the values written on the nodes.
Each of the next $$$n-1$$$ lines contain two integers $$$u$$$ and $$$v$$$ ($$$1\leq u, v\leq n$$$; $$$u\neq v$$$), denoting there is an undirected edge between node $$$u$$$ and node $$$v$$$. It is guaranteed that the given edges form a tree.
The next line contains an integer $$$q$$$ ($$$1\leq q\leq 2 \cdot 10^5$$$) — the number of queries.
Each of the next $$$q$$$ lines contains two integers $$$r$$$ and $$$v$$$ ($$$1\leq r, v\leq n$$$) — the root node Bob defines, and the node Alice chooses.
It is guaranteed that the sum of $$$n$$$ and the sum of $$$q$$$ over all test cases don't exceed $$$2 \cdot 10^5$$$.
For each test case, in each query, print a line containing an integer denoting the maximum score Bob can achieve.
3612 12 8 25 6 11 51 22 62 32 434 23 51 223 81 242 22 11 21 133 8 71 22 322 22 1
15 6 29 11 3 8 11 15 3
In each of the below figures, the green-colored node is the node picked by Bob, and the red-colored node is the node picked by Alice. The values of the nodes are placed in the blue boxes beside the nodes.
Consider the first example. In the first query, if we put the root node $$$4$$$ at the top of the tree, the tree looks like the below figure:
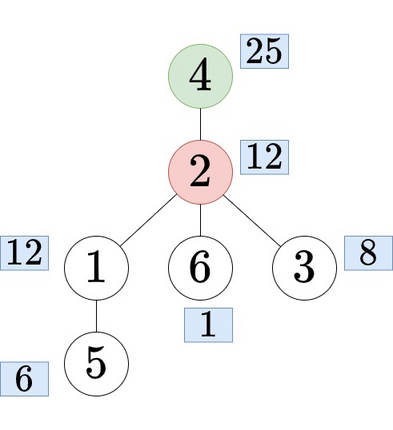 Tree with root node $$$4$$$ in the first query.
Tree with root node $$$4$$$ in the first query. In the second query, if the root node $$$3$$$ is placed at the top of the tree, the tree looks like the below figure:
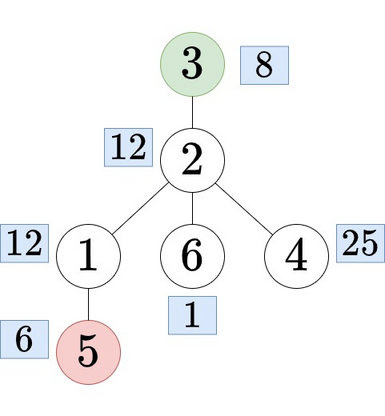 Tree with root node $$$3$$$ in the second query.
Tree with root node $$$3$$$ in the second query. In the third query, if the root node $$$1$$$ is placed at the top of the tree, the tree looks like this:
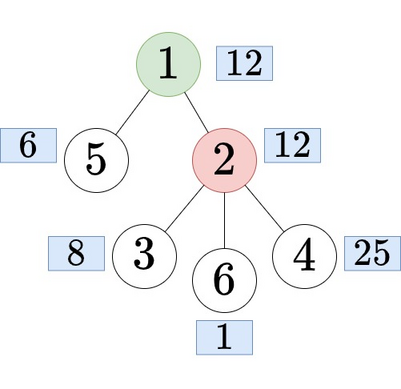 Tree with root node $$$1$$$ in the third query.
Tree with root node $$$1$$$ in the third query.
| Name |
|---|




