| Codeforces Round 848 (Div. 2) |
|---|
| Закончено |
Недавно на голову Боба с неба упало дерево. В дереве $$$n$$$ вершин. В каждой вершине $$$u$$$ дерева записано целое число $$$a_u$$$. В дереве нет фиксированного корня, так как оно упало с неба.
В настоящее время Боб изучает дерево. Чтобы внести некоторую изюминку, Алиса предлагает игру. Сначала Боб выбирает некоторую вершину $$$r$$$ корнем дерева. После этого Алиса выберет вершину $$$v$$$ и сообщит ее Бобу. Затем Боб выберет одну или несколько вершин из поддерева вершины $$$v$$$. Его результат будет равен побитовому исключающему ИЛИ всех значений, записанных в выбранных им вершинах. Боб должен сказать, какой максимальный результат он может получить для заданных $$$r$$$ и $$$v$$$.
Поскольку Боб не умеет решать задачи, он просит вас помочь ему найти ответ. Сможете ли вы ему помочь? Вам нужно найти ответ для нескольких комбинаций $$$r$$$ и $$$v$$$ для одного дерева.
Напомним, что дерево — это связный неориентированный граф без циклов. Поддерево вершины $$$u$$$ — это множество всех вершин $$$y$$$ таких, что простой путь от $$$y$$$ до корня проходит через $$$u$$$. Обратите внимание, что вершина $$$u$$$ входит в поддерево вершины $$$u$$$.
Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 10^5$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка содержит целое число $$$n$$$ ($$$2\leq n\leq 2 \cdot 10^5$$$) — количество вершин дерева.
Следующая строка содержит $$$n$$$ разделенных пробелами целых чисел $$$a_1, a_2, \dots, a_n$$$ ($$$1\leq a_i\leq 10^9$$$) — значения, записанные на вершинах.
Каждая из следующих $$$n-1$$$ строк содержит два целых числа $$$u$$$ и $$$v$$$ ($$$1\leq u, v\leq n$$$; $$$u\neq v$$$), обозначающих наличие неориентированного ребра между вершиной $$$u$$$ и вершиной $$$v$$$. Гарантируется, что данные ребра образуют дерево.
Следующая строка содержит целое число $$$q$$$ ($$$1\leq q\leq 2 \cdot 10^5$$$) — количество запросов.
Каждая из следующих $$$q$$$ строк содержит два целых числа $$$r$$$ и $$$v$$$ ($$$1\leq r, v\leq n$$$) — корневую вершину, которую определит Боб, и вершину, которую выберет Алиса.
Гарантируется, что сумма $$$n$$$ и сумма $$$q$$$ по всем наборам входных данных не превышают $$$2 \cdot 10^5$$$.
Для каждого набора входных данных для каждого запроса выведите строку, содержащую целое число, обозначающее максимальный результат, который может получить Боб.
3612 12 8 25 6 11 51 22 62 32 434 23 51 223 81 242 22 11 21 133 8 71 22 322 22 1
15 6 29 11 3 8 11 15 3
На каждом из приведенных ниже рисунков вершина, окрашенная в зеленый цвет — это вершина, выбранная Бобом, а вершина, окрашенный в красный цвет — это вершина, выбранная Алисой. Значения вершин помещены в синие ячейки рядом с вершинами.
Рассмотрим первый пример. В первом запросе, если мы примем вершину $$$4$$$ за корень, дерево будет выглядеть так, как показано на рисунке ниже:
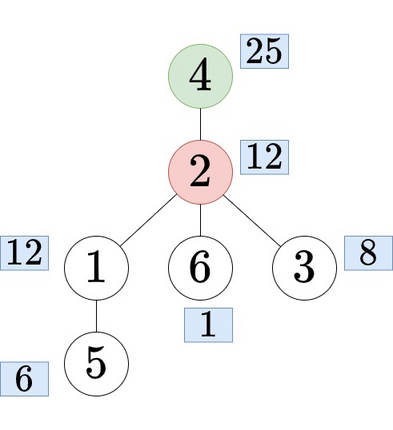 Дерево с корнем $$$4$$$ в первом запросе.
Дерево с корнем $$$4$$$ в первом запросе. Во втором запросе, если сделать корнем $$$3$$$, то дерево будет выглядеть так:
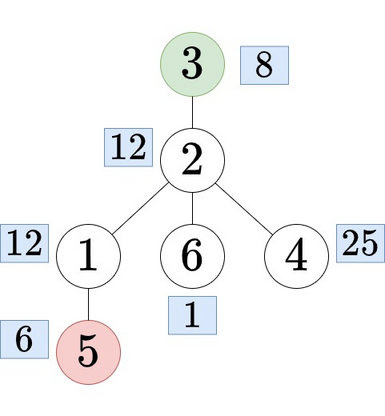 Дерево с корнем $$$3$$$ во втором запросе.
Дерево с корнем $$$3$$$ во втором запросе. В третьем запросе, если корень — $$$1$$$, то дерево выглядит следующим образом:
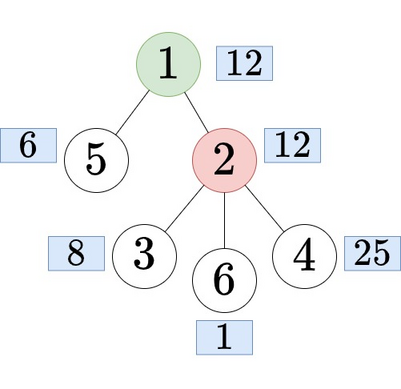 Дерево с корнем $$$1$$$ в третьем запросе.
Дерево с корнем $$$1$$$ в третьем запросе.
| Название |
|---|




