| ABBYY Cup 2.0 - Hard |
|---|
| Закончено |
Умный Бобер из ABBYY уже давно сотрудничает с НИИ «Цитологии и Генетики». Недавно работники этого НИИ предложили Бобру новую задачу. Суть задачи заключалась в следующем.
Есть набор из n белков (не обязательно различных). Каждый белок представляет собой строку, состоящую из маленьких букв латинского алфавита. Задача, которую поставили перед Умным Бобром ученые, заключается в выборе поднабора мощности k из исходного набора белков, причём репрезентативность выбранного поднабора белков должна быть максимальной.
Умный Бобер из ABBYY провел небольшое исследование и пришел к выводу, что репрезентативность набора белков можно оценить одним числом, которое достаточно просто вычисляется. Пусть у нас есть набор {a1, ..., ak} из k строк, описывающих белки. Репрезентативностью этого набора называется следующая величина:
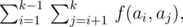
где f(x, y) — длина наибольшего общего префикса строк x и y; например, f(«abc», «abd») = 2, а f(«ab», «bcd») = 0.
Таким образом, репрезентативность набора белков {«abc», «abd», «abe»} равна 6, а набора {«aaa», «ba», «ba»} — 2.
После этого открытия Умный Бобер из ABBYY обратился к участникам Cup'а с просьбой написать программу, выбирающую из заданного набора белков поднабор мощности k, который имеет наибольшее возможное значение репрезентативности. Помогите ему с решением этой задачи!
Первая строка входных данных содержит два целых числа n и k (1 ≤ k ≤ n), разделенных единичным пробелом. Следующие n строк содержат описания белков по одному в строке. Каждый белок представляет собой непустую строку длиной не более 500 символов, состоящую только из строчных латинских букв (a...z). Строки могут совпадать.
Ограничения на входные данные для получения 20 баллов:
- 1 ≤ n ≤ 20
Ограничения на входные данные для получения 50 баллов:
- 1 ≤ n ≤ 100
Ограничения на входные данные для получения 100 баллов:
- 1 ≤ n ≤ 2000
Выведите одно целое число — наибольшее возможное значение репрезентативности поднабора мощности k заданного набора белков.
3 2
aba
bzd
abq
2
4 3
eee
rrr
ttt
qqq
0
4 3
aaa
abba
abbc
abbd
9
| Название |
|---|




