| VK Cup 2022 - Отборочный раунд (Engine) |
|---|
| Закончено |
В этой задаче мы будем работать с подвешенными бинарными деревьями. Напомним, что дерево называется подвешенным бинарным, если в нем есть выделенный корень, а у каждой вершины не более двух детей.
Сопоставим каждой вершине дерева один из двух цветов — белый или синий — и назовем такое сопоставление раскраской дерева. Раскраску назовем разнообразной, если у каждой вершины есть сосед (ребенок или родитель), покрашенный не в тот же цвет, что и сама вершина. Можно показать, что у любого дерева из не менее чем двух вершин существует разнообразная раскраска.
Дисбалансом раскраски назовем абсолютную разность между числом белых и синих вершин в ней.
Теперь к задаче. Изначально дерево состоит из одной вершины с номером $$$1$$$, являющейся его корнем. Далее для каждого $$$i$$$ от $$$2$$$ до $$$n$$$ в дереве появляется новая вершина $$$i$$$, которая становится ребенком вершины $$$p_i$$$. Гарантируется, что после каждого добавления дерево будет оставаться бинарным с корнем в вершине $$$1$$$, то есть у каждой вершины будет не более двух детей.
После каждого добавления вершины нужно вывести минимальное возможное значение дисбаланса по всем возможным разнообразным раскраскам текущего дерева. Более того, после добавления последней вершины с номером $$$n$$$ нужно также вывести саму разнообразную раскраску с минимальным дисбалансом.
Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$) — число вершин в итоговом дереве.
Вторая строка содержит $$$n-1$$$ целых чисел $$$p_2, p_3, \ldots, p_n$$$ ($$$1 \le p_i \le i - 1$$$) — номера родителей вершин $$$2, 3, \ldots, n$$$. Никакое число не встречается среди $$$p_2, p_3, \ldots, p_n$$$ более двух раз.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите $$$n-1$$$ целое число — минимальное возможное значение дисбаланса по всем возможным разнообразным раскраскам дерева после добавления в него вершин $$$2, 3, \ldots, n$$$.
Далее выведите строку из $$$n$$$ символов «w» и «b», описывающую разнообразную раскраску с минимальным дисбалансом для всего дерева целиком после добавления вершины $$$n$$$: $$$i$$$-й символ строки должен быть равен «w», если вершина $$$i$$$ покрашена в белый цвет, и «b», если в синий. Абсолютная разность между числом символов «w» и «b» должна быть равна последнему выведенному числу. У каждой вершины должен быть родитель или ребенок, покрашенный не в тот же цвет, что и сама вершина.
271 2 2 1 5 581 2 3 4 5 6 7
0 1 2 1 0 1 wbwwwbb 0 1 0 1 0 1 0 wbwbwbwb
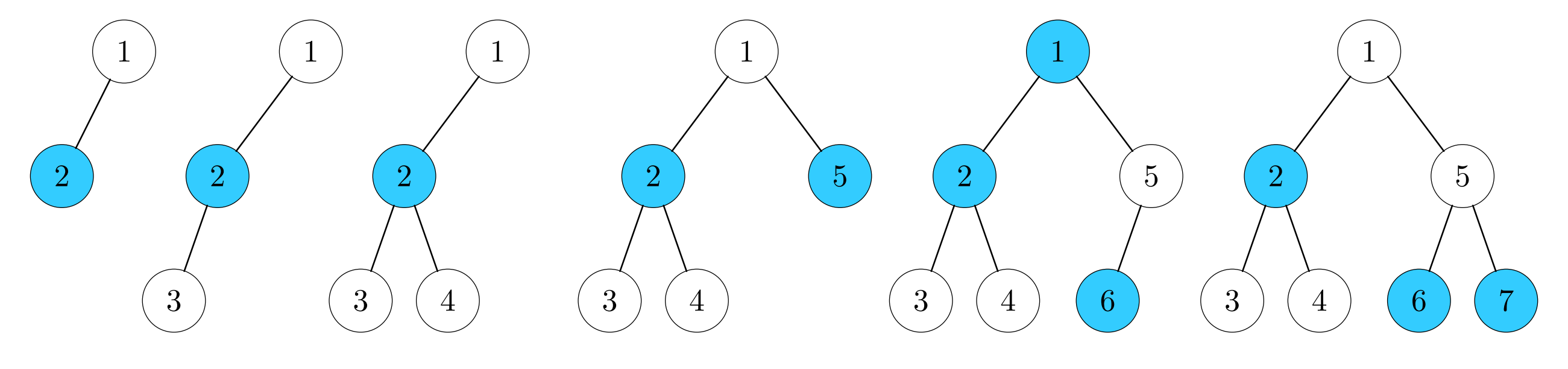
Примеры разнообразных раскрасок с минимальным дисбалансом для всех промежуточных деревьев в первом наборе входных данных представлены на рисунке ниже:
| Название |
|---|




