Перед вами прямоугольная таблица высоты $$$2$$$ и ширины $$$10^9$$$, состоящая из единичных клеток. На таблице расположено $$$n$$$ прямоугольников, причём границы прямоугольников проходят по границам клеток. $$$i$$$-й прямоугольник покрывает все клетки в строках с $$$u_i$$$ по $$$d_i$$$ включительно и столбцах с $$$l_i$$$ по $$$r_i$$$ включительно ($$$1 \le u_i \le d_i \le 2$$$; $$$1 \le l_i \le r_i \le 10^9$$$). Данные прямоугольники могут произвольным образом пересекаться, вкладываться и совпадать.
Вам нужно каждый прямоугольник либо удалить, либо заменить на любой свой непустой подпрямоугольник. Во втором случае подпрямоугольник должен целиком содержаться в исходном прямоугольнике, а его границы всё также должны проходить по границам клеток. При этом разрешается, чтобы подпрямоугольник совпал с исходным прямоугольником.
Требуется, чтобы никакие два (неудаленных) прямоугольника после замены не имели общих клеток, а суммарная площадь, покрытая новыми прямоугольниками, была как можно больше.
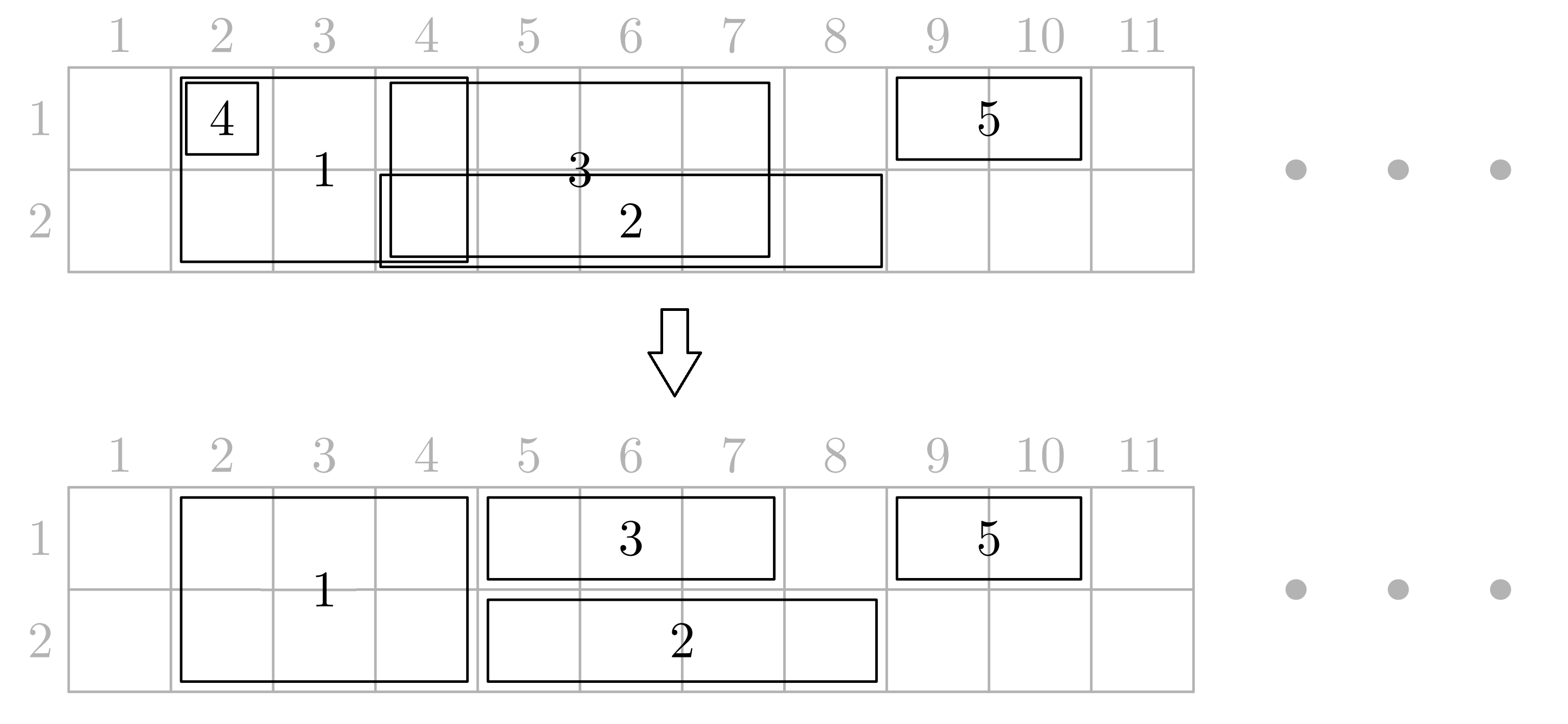Рисунок для первого набора входных данных. Сверху изображены данные прямоугольники, снизу — изменённые. Прямоугольник номер $$$4$$$ был удалён. Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ ($$$1 \le n \le 2 \cdot 10^5$$$) — количество прямоугольников.
Каждая из следующих $$$n$$$ строк содержит четыре целых числа $$$u_i, l_i, d_i, r_i$$$ ($$$1 \le u_i \le d_i \le 2$$$; $$$1 \le l_i \le r_i \le 10^9$$$) — координаты клеток, находящихся в левом верхнем и правом нижнем углу прямоугольника соответственно.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.
Для каждого набора входных данных сначала выведите целое число $$$s$$$ — максимальную возможную площадь, покрытую новыми прямоугольниками. Далее в $$$n$$$ строках выведите ваше решение для покрытия такой площади.
В $$$i$$$-й из этих строк выведите четыре целых числа $$$u'_i, l'_i, d'_i, r'_i$$$. Если вы удаляете $$$i$$$-й прямоугольник, выведите $$$u'_i = l'_i = d'_i = r'_i = 0$$$. Иначе эти числа обозначают новые координаты клеток в левом верхнем и правом нижнем углу $$$i$$$-го прямоугольника соответственно. Они должны удовлетворять следующим неравенствам: $$$u_i \le u'_i \le d'_i \le d_i$$$; $$$l_i \le l'_i \le r'_i \le r_i$$$.
Если существует несколько решений, выведите любое из них.
851 2 2 42 4 2 81 4 2 71 2 1 21 9 1 1021 1 1 101 5 1 1521 1 1 101 1 1 1051 3 1 71 3 1 81 1 1 41 2 1 71 10 1 1121 1 2 101 5 1 821 5 2 101 2 1 721 5 2 102 2 2 1552 6 2 71 4 2 51 5 1 91 7 2 101 2 1 6
15 1 2 2 4 2 5 2 8 1 5 1 7 0 0 0 0 1 9 1 10 15 1 1 1 10 1 11 1 15 10 1 1 1 10 0 0 0 0 10 0 0 0 0 1 8 1 8 1 1 1 4 1 5 1 7 1 10 1 11 20 1 1 2 10 0 0 0 0 15 1 5 2 10 1 2 1 4 20 1 5 1 10 2 2 2 15 16 2 6 2 6 2 4 2 5 0 0 0 0 1 7 2 10 1 2 1 6
На рисунке в условии задачи изображен первый набор входных данных.
