Вам задано дерево из $$$n$$$ вершин и $$$n - 1$$$ ребра. Первоначальный вес $$$i$$$-й вершины равен $$$a_i$$$.
Назовем расстоянием $$$d_v(u)$$$ от вершины $$$v$$$ до вершины $$$u$$$ количество ребер на пути из $$$v$$$ в $$$u$$$. Заметим, что $$$d_v(u) = d_u(v)$$$ и $$$d_v(v) = 0$$$.
Назовем взвешенным расстоянием $$$w_v(u)$$$ от $$$v$$$ до $$$u$$$ значение $$$w_v(u) = d_v(u) + a_u$$$. Заметим, что $$$w_v(v) = a_v$$$ и $$$w_v(u) \neq w_u(v)$$$, если $$$a_u \neq a_v$$$.
Аналогично обычному расстоянию, назовем эксцентриситетом $$$e(v)$$$ вершины $$$v$$$ наибольшее взвешенное расстояние от $$$v$$$ до какой-либо вершины (включая саму $$$v$$$), или $$$e(v) = \max\limits_{1 \le u \le n}{w_v(u)}$$$.
Наконец, назовем радиусом $$$r$$$ дерева наименьший из эксцентриситетов его вершин, или $$$r = \min\limits_{1 \le v \le n}{e(v)}$$$.
Вам нужно обработать $$$m$$$ запросов следующего вида:
- $$$v_j$$$ $$$x_j$$$ — присвоить $$$a_{v_j} = x_j$$$.
После обработки каждого запроса выведите радиус $$$r$$$ текущего дерева.
В первой строке задано одно целое число $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$) — количество вершин в дереве.
Во второй строке заданы $$$n$$$ целых чисел $$$a_1, \dots, a_n$$$ ($$$0 \le a_i \le 10^6$$$) — первоначальные веса вершин.
В следующих $$$n - 1$$$ строках заданы ребра дерева. В $$$i$$$-й строке заданы два целых числа $$$u_i$$$ и $$$v_i$$$ ($$$1 \le u_i, v_i \le n$$$; $$$u_i \neq v_i$$$) — соответствующее ребро. Заданные ребра образуют дерево.
В следующей строке задано одно целое число $$$m$$$ ($$$1 \le m \le 10^5$$$) — количество запросов.
В следующих $$$m$$$ строках заданы сами запросы — по одному в строке. В $$$j$$$-м запросе заданы два целых числа $$$v_j$$$ и $$$x_j$$$ ($$$1 \le v_j \le n$$$; $$$0 \le x_j \le 10^6$$$) — вершина и ее новый вес.
Выведите $$$m$$$ целых чисел — радиус $$$r$$$ дерева после обработки каждого запроса.
6 1 3 3 7 0 1 2 1 1 3 1 4 5 4 4 6 5 4 7 4 0 2 5 5 10 5 5
7 4 5 10 7
После первого запроса дерево выглядит следующим образом:
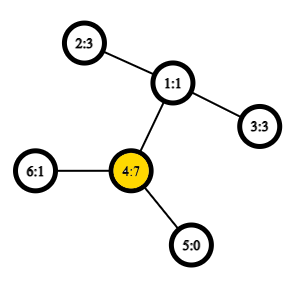
Дерево после второго запроса:
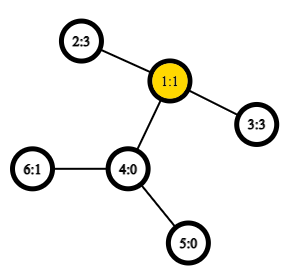
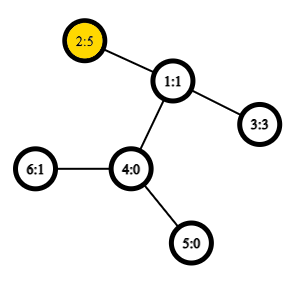
После третьего запроса радиус $$$r = e(2) = 5$$$:
| Название |
|---|




