C. Дегустация чая
ограничение по времени на тест
2 секунды
ограничение по памяти на тест
256 мегабайт
ввод
стандартный ввод
вывод
стандартный вывод

Производитель чая рашил организовать огромную церемонию дегустации чая. $$$n$$$ дегустаторов будут пробовать $$$n$$$ сортов чая. И сорта чая, и дегустаторы пронумерованы от $$$1$$$ до $$$n$$$. Производитель подготовил $$$a_i$$$ миллилитров $$$i$$$-го сорта чая. $$$j$$$-й дегустатор способен выпить $$$b_j$$$ миллилитров чая за раз.

Дегустация будет происходить по этапам. На первом этапе $$$i$$$-й дегустатор попробует $$$i$$$-й сорт чая. $$$i$$$-й дегустатор выпивает $$$\min(a_i, b_i)$$$ чая (сколько доступно $$$i$$$-го сорта чая и сколько $$$i$$$-й дегустатор способен выпить). $$$a_i$$$ также уменьшается на это количество.

Затем все дегустаторы переходят к предыдущему сорту чая. Тогда на втором этапе $$$i$$$-й дегустатор пробует $$$(i-1)$$$-й сорт чая. $$$i$$$-й дегустатор выпивает $$$\min(a_{i-1}, b_i)$$$ чая. $$$1$$$-й дегустатор заканчивает дегустацию.

На третьем этапе $$$i$$$-й дегустатор пробует $$$(i-2)$$$-й сорт чая. $$$2$$$-й дегустатор заканчивает дегустацию. Это продолжается, пока все дегустаторы не закончат дегустацию.

Рассмотрим процесс дегустации для $$$n = 3$$$, $$$a = [10, 20, 15]$$$, $$$b = [9, 8, 6]$$$. В левом столбце записаны текущие количества каждого сорта чая. В правом столбце записаны текущие выпитые количества чая для каждого дегустатора. Стрелка указывает, какой дегустатор пьет каждый чай на текущем шаге. Число на стрелке — это количество — минимум из того, сколько доступно сорта чая, и того, сколько может выпить дегустатор.

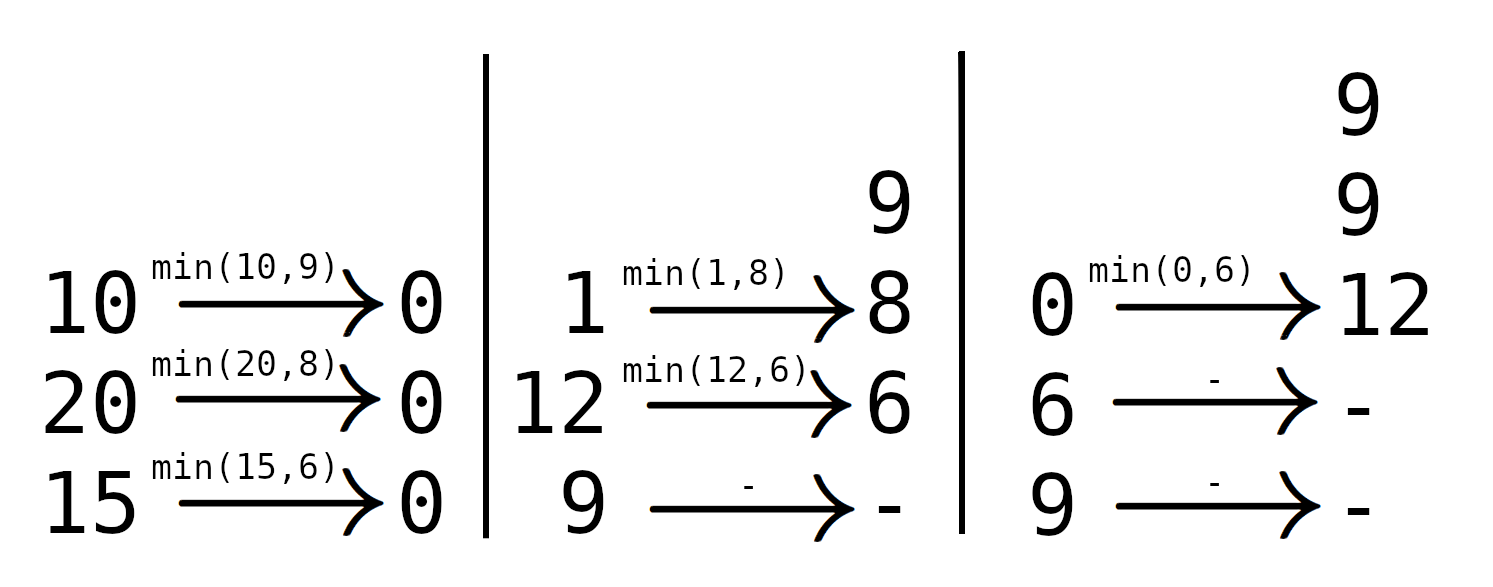
Для каждого дегустатора выведите, сколько миллилитров чая он/она суммарно выпьет.

Входные данные

В первой строке записано целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных.

В первой строке каждого набора входных данных записано одно целое число $$$n$$$ ($$$1 \le n \le 2 \cdot 10^5$$$) — количество сортов чая и количество дегустаторов.

Во второй строке записаны $$$n$$$ целых чисел $$$a_1, a_2, \dots, a_n$$$ ($$$1 \le a_i \le 10^9$$$) — количество каждого сорта чая.

В третьей строке записаны $$$n$$$ целых чисел $$$b_1, b_2, \dots, b_n$$$ ($$$1 \le b_i \le 10^9$$$) — количество чая, которое каждый дегустатор может выпить за раз.

Сумма $$$n$$$ по всем наборам входных данных не превосходит $$$2 \cdot 10^5$$$.

Выходные данные

На каждый набор входных данных выведите $$$n$$$ целых чисел — $$$i$$$-е значение должно быть равно суммарному количеству чая, выпитому $$$i$$$-м дегустатором.

Пример
Входные данные
4
3
10 20 15
9 8 6
1
5
7
4
13 8 5 4
3 4 2 1
3
1000000000 1000000000 1000000000
1 1 1000000000
Выходные данные
9 9 12 
5 
3 8 6 4 
1 2 2999999997
Примечание

Первый набор входных данных описан в условии. Здесь предоставлены оставшиеся количества каждого сорта чая после каждого этапа и количество выпитого каждым дегустатором чая:

  • $$$a = [1, 12, 9]$$$, $$$\mathit{ans} = [9, 8, 6]$$$
  • $$$a = [0, 6, 9]$$$, $$$\mathit{ans} = [9, 9, 12]$$$
  • $$$a = [0, 6, 9]$$$, $$$\mathit{ans} = [9, 9, 12]$$$

Во втором наборе входных данных единственный дегустатор выпьет $$$\min(5, 7)$$$ миллилитров чая единственного сорта.

Здесь предоставлены оставшиеся количества каждого сорта чая после каждого этапа и количество выпитого каждым дегустатором чая для третьего набора входных данных:

  • $$$a = [10, 4, 3, 3]$$$, $$$\mathit{ans} = [3, 4, 2, 1]$$$;
  • $$$a = [6, 2, 2, 3]$$$, $$$\mathit{ans} = [3, 8, 4, 2]$$$;
  • $$$a = [4, 1, 2, 3]$$$, $$$\mathit{ans} = [3, 8, 6, 3]$$$;
  • $$$a = [3, 1, 2, 3]$$$, $$$\mathit{ans} = [3, 8, 6, 4]$$$.

Здесь предоставлены оставшиеся количества каждого сорта чая после каждого этапа и количество выпитого каждым дегустатором чая для четвертого набора входных данных:

  • $$$a = [999999999, 999999999, 0]$$$, $$$\mathit{ans} = [1, 1, 1000000000]$$$;
  • $$$a = [999999998, 0, 0]$$$, $$$\mathit{ans} = [1, 2, 1999999999]$$$;
  • $$$a = [0, 0, 0]$$$, $$$\mathit{ans} = [1, 2, 2999999997]$$$.