| Codeforces Round 864 (Div. 2) |
|---|
| Закончено |
У Li Hua есть дерево с $$$n$$$ вершинами и $$$n-1$$$ ребром. Корнем дерева является вершина $$$1$$$. Каждая вершина $$$i$$$ имеет важность $$$a_i$$$. Обозначим размер поддерева как количество вершин в нем, а важность как сумму важности вершин в нем. Обозначим тяжелым сыном нелистовой вершины сына с наибольшим размером поддерева. Если таких вершин несколько, то тяжёлым сыном будет та, у которой индекс минимален.
Li Hua хочет выполнить $$$m$$$ операций:
- «1 $$$x$$$» ($$$1\leq x \leq n$$$) — вычислить важность поддерева, корнем которого является $$$x$$$.
- «2 $$$x$$$» ($$$2\leq x \leq n$$$) — повернуть тяжёлого сына поддерева $$$x$$$ вверх. Формально, обозначим как $$$son_x$$$ тяжелого сына $$$x$$$, $$$fa_x$$$ как отца $$$x$$$. Он хочет удалить ребро между $$$x$$$ и $$$fa_x$$$ и добавить ребро между $$$son_x$$$ и $$$fa_x$$$. Гарантируется, что $$$x$$$ не является корнем, но не гарантируется, что $$$x$$$ не является листом. Если $$$x$$$ является листом, проигнорируйте эту операцию.
Предположим, что вы Li Hua. Пожалуйста, решите эту задачу.
Первая строка содержит 2 целых числа $$$n,m$$$ ($$$2\le n\le 10^{5},1\le m\le 10^{5}$$$) — количество вершин в дереве и количество операций.
Вторая строка содержит $$$n$$$ целых чисел $$$a_{1},a_{2},\ldots ,a_{n}$$$ ($$$-10^{9}\le a_{i}\le 10^{9}$$$) — важность каждой вершины.
Следующие $$$n-1$$$ строк содержат рёбра дерева. В $$$i$$$-й строке записаны два целых числа $$$u_i$$$ и $$$v_i$$$ ($$$1\le u_i,v_i\le n$$$, $$$u_i\ne v_i$$$) — соответствующее ребро. Данные рёбра образуют дерево.
Следующие $$$m$$$ строк содержат операции — по одной операции в строке. $$$j$$$-я операция содержит два целых числа $$$t_{j},x_{j}$$$ ($$$t_{j}\in \{1,2\}$$$, $$$1 \leq x_{j} \leq n$$$, $$$x_{j}\neq 1$$$ если $$$t_j = 2$$$) — $$$j$$$-я операция.
Для каждого запроса вида «1 $$$x$$$» выведите ответ в отдельной строке.
7 4 1 1 1 1 1 1 1 1 2 1 3 2 4 2 5 3 6 6 7 1 6 2 3 1 6 1 2
2 3 3
10 14 -160016413 -90133231 -671446275 -314847579 -910548234 121155052 -359359950 83112406 -704889624 145489303 1 6 1 10 10 8 1 4 3 4 2 7 2 5 3 2 9 8 1 4 2 2 2 4 1 4 1 10 2 10 1 9 1 6 2 8 2 10 1 5 1 8 1 1 2 5
-2346335269 -314847579 -476287915 -704889624 121155052 -1360041415 228601709 -2861484545
В первом примере:
Начальное дерево показано на следующем рисунке:
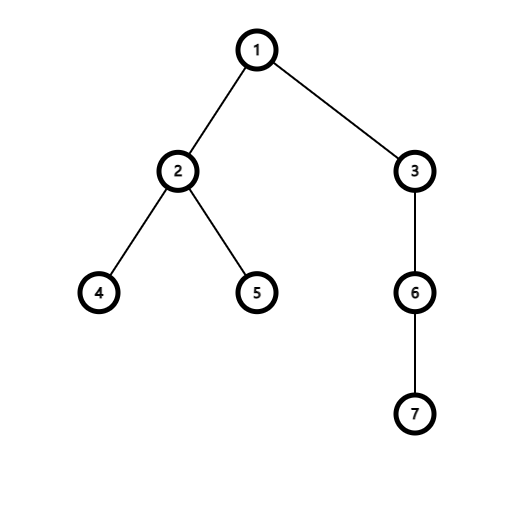 |
Важность поддерева $$$6$$$ равна $$$a_6+a_7=2$$$.
После поворота тяжелого сына вершины $$$3$$$ (которым является $$$6$$$) вверх, дерево будет выглядеть следующим образом:
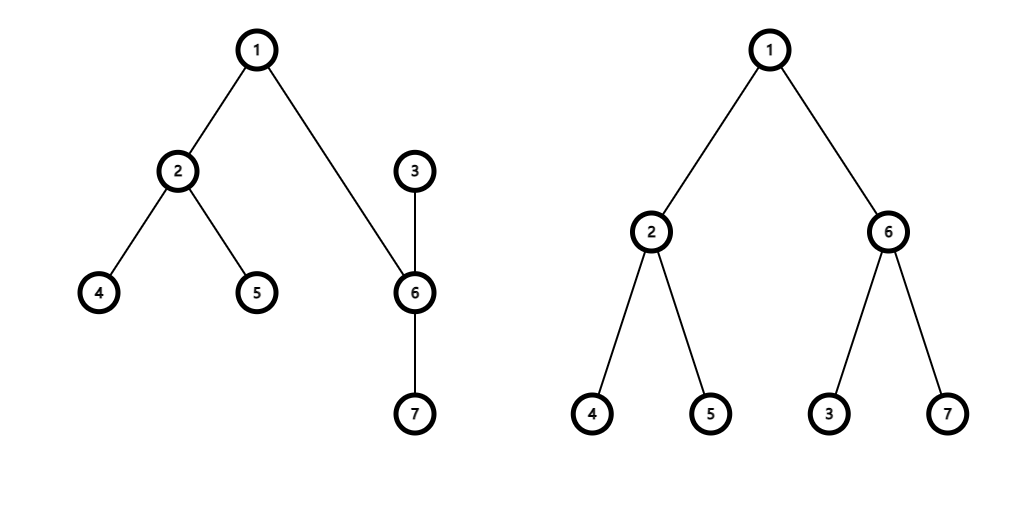 |
Важность поддерева $$$6$$$ равна $$$a_6+a_3+a_7=3$$$.
Важность поддерева $$$2$$$ - $$$a_2+a_4+a_5=3$$$.
| Название |
|---|




