| Codeforces Round 862 (Div. 2) |
|---|
| Закончено |
Вселенная представляет собой координатную плоскость. На ней проложено $$$n$$$ космических трасс, каждая из которых представляет собой прямую $$$y=kx$$$, проходящую через начало координат $$$(0, 0)$$$. Также там есть $$$m$$$ астероидных поясов, которые представляют собой параболы ветвями вверх, их можно представить как графики функций $$$y=ax^2+bx+c$$$, где $$$a > 0$$$.
Вы хотите сфотографировать каждую параболу. Для этого для каждой параболы вам нужно выбрать прямую, которая не пересекается с этой параболой и не касается её. Вы можете выбирать одну и ту же прямую для нескольких парабол. Найдите для каждой параболы такую прямую или определите, что её нет.
Каждый тест состоит из нескольких наборов входных данных. В первой строке содержится одно число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
В первой строке каждого набора даны $$$2$$$ целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n, m \le 10^5$$$) — количество прямых и парабол соответственно.
Далее в $$$n$$$ строках содержится по одному целому числу $$$k$$$ ($$$|k| \le 10^8$$$) — коэффициенты уравнений прямых $$$y=kx$$$, описывающих прямые. Прямые могут совпадать, $$$k$$$ может быть равно $$$0$$$.
Далее в $$$m$$$ строках содержится по $$$3$$$ целых числа $$$a$$$, $$$b$$$ и $$$c$$$ ($$$a, |b|, |c| \le 10^8$$$, $$$a > 0$$$) — коэффициенты уравнений парабол $$$ax^2+bx+c$$$. Параболы могут совпадать.
Гарантируется, что сумма $$$n$$$ по всем наборам не превосходит $$$10^5$$$ и сумма $$$m$$$ по всем наборам также не превосходит $$$10^5$$$.
Для каждого набора входных данных выведите ответ для каждой параболы в данном порядке. Если в данном наборе есть прямая, не пересекающаяся с данной параболой и не касающаяся ее, выведите сначала в отдельной строке слово «YES», а далее в отдельной строке число $$$k$$$ — коэффициент этой прямой. Если таких прямых несколько, выведите любую из них. Если же искомой прямой нет, выведите одно слово «NO».
Вы можете выводить каждую букву в любом регистре (строчную или заглавную). Например, строки «yEs», «yes», «Yes» и «YES» будут приняты как положительный ответ.
Пустые строки в выводе в примере даны только для наглядности, вам их выводить необязательно (но можно).
51 211 -1 21 -1 32 2141 2 12 5 11 101 0 01 1100000000100000000 100000000 1000000002 3022 2 11 -2 11 -2 -1
YES 1 YES 1 YES 1 YES 4 NO YES 100000000 YES 0 NO NO
В первом наборе входных данных обе параболы не пересекаются с единственной данной прямой $$$y=1\cdot x$$$, поэтому ответом будет два числа $$$1$$$.
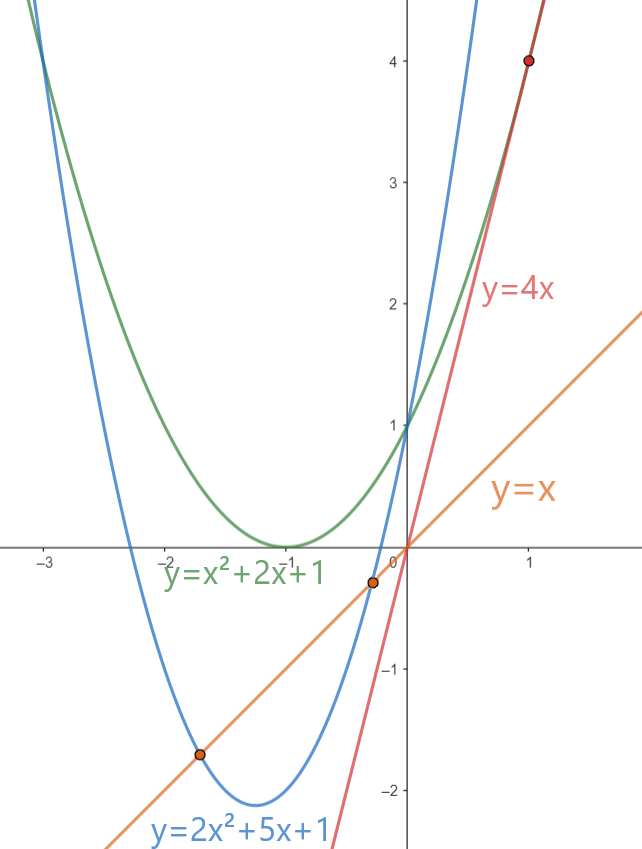
Во втором наборе прямая $$$y=x$$$ и парабола $$$2x^2+5x+1$$$ пересекаются, а также прямая $$$y=4x$$$ и парабола $$$x^2+2x+1$$$ касаются, поэтому эти пары не удовлетворяют условию. Значит, для первой параболы ответом будет $$$1$$$ ($$$y=1x$$$), а для второй параболы — $$$4$$$.
В третьем тестовом наборе прямая и парабола пересекаются, поэтому ответ — «NO».
| Название |
|---|




