| Codeforces Round 859 (Div. 4) |
|---|
| Закончено |
Вам дана комната, которую можно представить в виде сетки из $$$n \times m$$$. В позиции $$$(i_1, j_1)$$$ (пересечение строки $$$i_1$$$ и столбца $$$j_1$$$) находится шар, который начинает двигаться по диагонали в одном из четырех направлений:
- Шарик движется вниз и вправо, обозначается $$$\texttt{DR}$$$; это означает, что после шага местоположение шарика изменяется с $$$(i, j)$$$ на $$$(i+1, j+1)$$$.
- Мяч движется вниз и влево, обозначается $$$\texttt{DL}$$$; это означает, что после шага местоположение мяча изменяется с $$$(i, j)$$$ на $$$(i+1, j-1)$$$.
- Мяч движется вверх и вправо, обозначается $$$\texttt{UR}$$$; это означает, что после шага местоположение мяча изменяется с $$$(i, j)$$$ на $$$(i-1, j+1)$$$.
- Мяч движется вверх и влево, обозначается $$$\texttt{UL}$$$; это означает, что после шага местоположение мяча изменяется с $$$(i, j)$$$ на $$$(i-1, j-1)$$$.
После каждого шага мяч сохраняет свое направление, если только он не ударится о стену (то есть направление выведет его за пределы комнаты на следующем шаге). В этом случае направление мяча изменяется вдоль оси стены; если мяч попадает в угол, то изменяются оба направления. Любой такой случай называется отскоком. Мяч никогда не перестает двигаться.
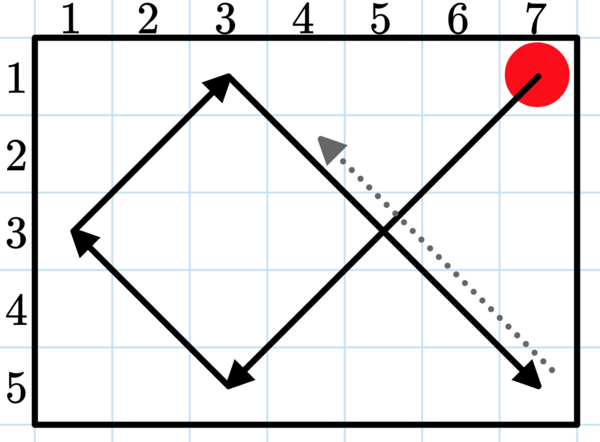
В приведенном примере мяч стартует с точки $$$(1, 7)$$$ и движется в направлении $$$\texttt{DL}$$$, пока не достигнет нижней стены, затем он подпрыгивает и продолжает движение в направлении $$$\texttt{UL}$$$. Достигнув левой стены, мяч подпрыгивает и продолжает двигаться в направлении $$$\texttt{UR}$$$. Когда мяч достигает верхней стены, он подпрыгивает и продолжает движение в направлении $$$\texttt{DR}$$$. Достигнув правого нижнего угла, он отскакивает один раз и продолжает движение в направлении $$$\texttt{UL}$$$, и так далее.
Ваша задача - найти, сколько отскоков произойдёт, пока мяч не достигнет клетки $$$(i_2, j_2)$$$ в комнате, или сообщить, что он никогда не достигнет клетки $$$(i_2, j_2)$$$, выведя $$$-1$$$.
Обратите внимание, что мяч сначала попадает в клетку и только после этого отскакивает, если это происходит.
Первая строка содержит одно целое число $$$t$$$ ($$$1 \leq t \leq 1000$$$) — количество наборов входных данных.
Первая строка каждого набора входных данных содержит шесть целых чисел и строку $$$n, m, i_1, j_1, i_2, j_2, d$$$ ($$$2 \leq n, m \leq 25000$$$; $$$1 \leq i_1, i_2 \leq n$$$; $$$1 \leq j_1, j_2 \leq m$$$; $$$d \in\{ \texttt{DR}, \texttt{DL}, \texttt{UR}, \texttt{UL}\}$$$) — размеры сетки, начальные координаты шарика, координаты конечной клетки и начальное направление шарика.
Гарантируется, что сумма $$$n \cdot m$$$ по всем наборам входных данных не превосходит $$$5 \cdot 10^4$$$.
Для каждого набора входных данных выведите одно целое число — количество отскоков мяча, пока он не достигнет клетки $$$(i_2, j_2)$$$ в первый раз, или $$$-1$$$, если мяч никогда не достигнет данной клетки.
65 7 1 7 2 4 DL5 7 1 7 3 2 DL3 3 1 3 2 2 UR2 4 2 1 2 2 DR4 3 1 1 1 3 UL6 4 1 2 3 4 DR
3 -1 1 -1 4 0
| Название |
|---|




