| Codeforces Round 863 (Div. 3) |
|---|
| Закончено |
Конвейерная матрица $$$m_n$$$ — матрица размера $$$n \times n$$$, $$$n$$$ — чётное число. Матрица состоит из концентрических лент, движущихся по часовой стрелке.
Иными словами, конвейерная матрица для $$$n = 2$$$ — это просто матрица $$$2 \times 2$$$, ячейки которой образуют цикл длины $$$4$$$ по часовой стрелке. Для любого натурального $$$k \ge 2$$$, матрица $$$m_{2k}$$$ получается добавлением к матрице $$$m_{2k - 2}$$$ внешнего слоя, образующего цикл, направленный по часовой стрелке.
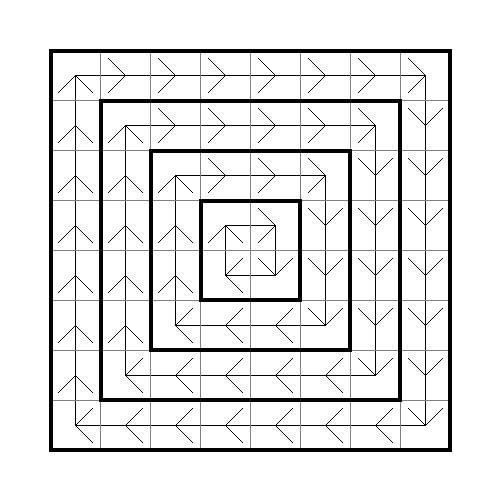 Конвейерная матрица $$$8 \times 8$$$.
Конвейерная матрица $$$8 \times 8$$$. Вы стоите в ячейке с координатами $$$x_1, y_1$$$ и хотите попасть в ячейку с координатами $$$x_2, y_2$$$. Клетка имеет координаты $$$x, y$$$, если находится на пересечении $$$x$$$-й строки и $$$y$$$-го столбца.
Стоя на какой-то ячейке, вы каждую секунду будете перемещаться на ячейку, следующую в направлении движения ленты, на которой вы находитесь. Также вы можете переместиться на соседнюю ячейку, потратив одну единицу энергии. Перемещения происходят мгновенно и их можно совершать неограниченное количество в любой момент времени.
Ваша задача — найти минимальное количество энергии, которое придётся потратить, чтобы добраться из ячейки с координатами $$$x_1, y_1$$$ в ячейку с координатами $$$x_2, y_2$$$.
Например, $$$n=8$$$ изначально вы находитесь в ячейке с координатами $$$1,3$$$ и хотите попасть в ячейку с координатами $$$6, 4$$$. Вы можете сразу же сделать $$$2$$$ перемещения, оказавшись в ячейке с координатами $$$3, 3$$$, а затем через $$$8$$$ секунд вы окажетесь в нужной ячейке.
Первая строка содержит целое число $$$t$$$ ($$$1 \le t \le 2 \cdot 10^5$$$) — количество наборов входных данных.
Далее следуют описания наборов входных данных.
Описание каждого набора входных данных состоит из одной строки, содержащей пять целых чисел $$$n$$$, $$$x_1$$$, $$$y_1$$$, $$$x_2$$$ и $$$y_2$$$ ($$$1 \le x_1, y_1, x_2, y_2 \le n \le 10^9$$$) — размер матрицы и координаты начальной и конечной ячеек. Гарантируется, что число $$$n$$$ четно.
Для каждого набора входных данных в отдельной строке выведите одно целое число — минимальное количество энергии, которое придётся потратить, чтобы добраться из ячейки с координатами $$$x_1, y_1$$$ в ячейку с координатами $$$x_2, y_2$$$.
52 1 1 2 24 1 4 3 38 1 3 4 6100 10 20 50 1001000000000 123456789 987654321 998244353 500000004
0 1 2 9 10590032
| Название |
|---|




