| Codeforces Round 865 (Div. 2) |
|---|
| Закончено |
Лягушки Ян и Мэри живут в точках целочисленной решётки декартовой координатной плоскости, Ян живёт в $$$(0,0)$$$, Мэри живёт в $$$(a,b)$$$.
Ян хочет навестить Мэри, прыгая по декартовой координатной плоскости. Каждую секунду он прыгает из его текущей позиции $$$(x_p, y_p)$$$ в другую целочисленную точку $$$(x_q, y_q)$$$, такую, что никакая другая целочисленная точка, кроме $$$(x_p, y_p)$$$ и $$$(x_q, y_q)$$$, не лежит на отрезке между точками $$$(x_p, y_p)$$$ и $$$(x_q, y_q)$$$.
Так как Ян хочет встретить Мэри как можно быстрее, он хочет допрыгать до точки $$$(a,b)$$$, используя не более $$$2$$$ прыжков. К сожалению, Ян плох в математике. Можете ему помочь?
Точка целочисленной решётки определяется как точка, у которой $$$x$$$-координата и $$$y$$$-координата являются целыми числами.
Первая строка содержит одно целое число $$$t$$$ ($$$1 \le t \le 500$$$) — количество наборов входных данных. Далее следует описание наборов.
Первая и единственная строка каждого набора входных данных содержит два целых числа $$$a$$$ и $$$b$$$ ($$$1\le a,b\le 10^9$$$) — координаты целочисленной точки, где живёт Мэри.
Для каждого набора входных данных выведите целое число $$$n$$$ ($$$1 \le n \le 2$$$) в первой строке — количество прыжков, которые сделает Ян для встречи с Мэри. Обратите внимание, что вам не нужно минимизировать количество прыжков.
В $$$i$$$-й из следующих $$$n$$$ строк, выведите два целых числа $$$0 \le x_i,y_i \le 10^9$$$, разделённых пробелом, обозначающих координаты $$$(x_i,y_i)$$$ Яна после $$$i$$$-го прыжка. Должно выполняться условие $$$x_n = a$$$, $$$y_n = b$$$.
Начальное местоположение Яна и его местоположение после каждого из $$$n$$$ прыжков не обязательно должны быть разными.
Если существует несколько решений, выведите любое из них.
83 44 43 62 21 17 32022 20231000000000 1000000000
1 3 4 2 3 2 4 4 2 5 3 3 6 2 1 0 2 2 1 1 1 1 7 3 1 2022 2023 2 69420420 469696969 1000000000 1000000000
В первом наборе входных данных:
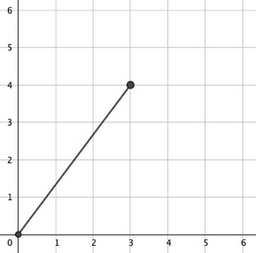
$$$(0,0) \to (3,4)$$$
Во втором наборе входных данных:
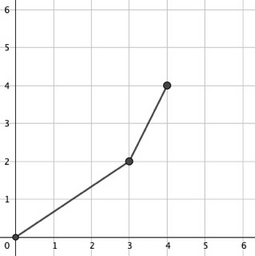
$$$(0,0) \to (3,2) \to (4,4)$$$
В третьем наборе входных данных:
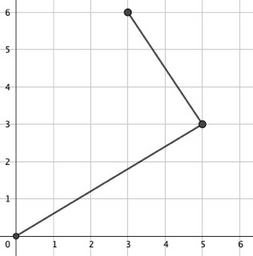
$$$(0,0) \to (5,3) \to (3,6)$$$
| Название |
|---|




