| Codeforces Round 869 (Div. 1) |
|---|
| Закончено |
Дан простой неориентированный граф с $$$n$$$ вершинами и $$$m$$$ ребрами. Граф может не быть связным. Вершины графа пронумерованы от $$$1$$$ до $$$n$$$.
Граф-рыба — это граф, содержащий простой цикл с особой вершиной $$$u$$$, принадлежащей циклу. Помимо ребер цикла, у графа должно быть ровно $$$2$$$ дополнительных ребра. Оба ребра должны быть соединены с вершиной $$$u$$$, но не должны быть соединены с любой другой вершиной цикла.
Определите, содержит ли данный граф подграф-рыбу, и если да, найдите любой такой подграф.
В этой задаче подграф определяется как граф, полученный путем выбора любого подмножества ребер исходного графа.
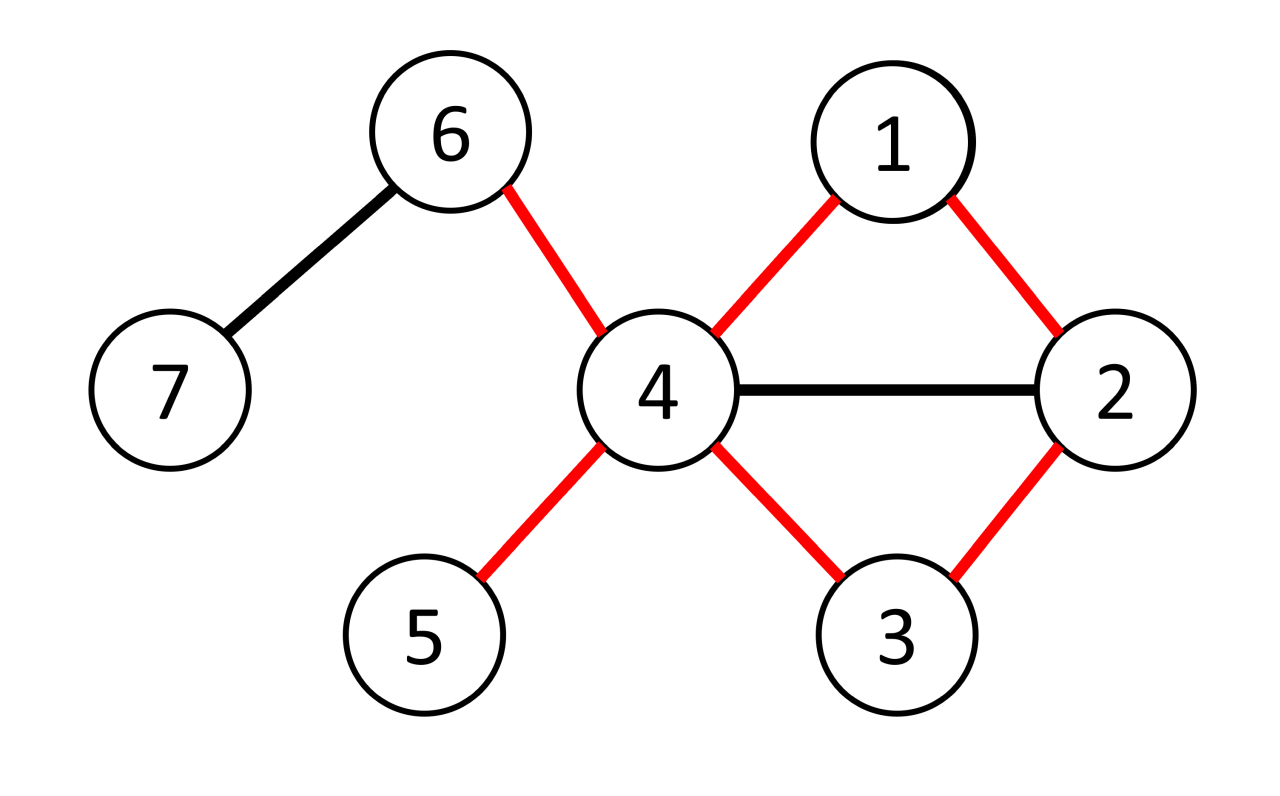 Визуализация примера 1. Красные ребра образуют один из возможных подграфов, который является графом-рыбой.
Визуализация примера 1. Красные ребра образуют один из возможных подграфов, который является графом-рыбой. Каждый тест состоит из нескольких наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \leq t \leq 1000$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит два целых числа, $$$n$$$ и $$$m$$$ ($$$1 \le n, m \le 2\,000$$$) — количество вершин и количество ребер.
Каждая из следующих $$$m$$$ строк содержит описание ребра. Каждая строка содержит два целых числа $$$u_i$$$ и $$$v_i$$$ ($$$1 \leq u_i, v_i \leq n$$$, $$$u_i\neq v_i$$$) — ребро соединяет вершину $$$u_i$$$ с вершиной $$$v_i$$$.
Гарантируется, что никакие два ребра не соединяют одну и ту же неупорядоченную пару вершин.
Кроме того, гарантируется, что сумма $$$n$$$ и сумма $$$m$$$ для всех наборов входных данных не превышает $$$2\,000$$$.
Для каждого набора входных данных выведите «YES», если граф содержит подграф-рыбу, в противном случае выведите «NO». Если ответ «YES», на следующих строках выведите описание подграфа.
Первая строка описания содержит одно целое число $$$k$$$ — количество ребер подграфа.
В следующих $$$k$$$ строках выведите ребра выбранного подграфа. Каждая из $$$k$$$ строк должна содержать два целых числа $$$u$$$ и $$$v$$$ ($$$1\le u, v\le n$$$, $$$u\neq v$$$) — ребро между $$$u$$$ и $$$v$$$ принадлежит подграфу. Порядок, в котором выводятся $$$u$$$ и $$$v$$$, не имеет значения, если эти две вершины соединены ребром в исходном графе. Порядок вывода ребер не имеет значения, если полученный подграф является графом-рыбой.
Если есть несколько решений, выведите любое.
37 81 22 33 44 14 54 64 26 77 76 71 22 33 44 11 33 54 41 33 44 11 2
YES 6 5 4 6 4 4 3 1 4 2 1 3 2 YES 5 5 3 2 3 3 1 4 3 1 4 NO
В первом примере возможный допустимый подграф содержит цикл $$$1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \rightarrow 1$$$. Особой вершиной этого цикла является вершина $$$4$$$. Два дополнительных ребра $$$4 - 5$$$ и $$$4 - 6$$$ оба соединены с $$$4$$$, образуя граф-рыбу.
Во втором примере возможный допустимый подграф содержит цикл $$$1 \rightarrow 3 \rightarrow 4 \rightarrow 1$$$. Особой вершиной этого цикла является вершина $$$3$$$. Два дополнительных ребра $$$3 - 2$$$ и $$$3 - 5$$$ оба соединены с $$$3$$$, образуя граф-рыбу.
В последнем примере можно доказать, что у графа нет подграфа-рыбы.
| Название |
|---|




