F. Случайная прогулка
ограничение по времени на тест
2 секунды
ограничение по памяти на тест
256 мегабайт
ввод
стандартный ввод
вывод
стандартный вывод

Вам задано дерево, состоящее из $$$n$$$ вершин и $$$n - 1$$$ ребер, и у каждой вершины $$$v$$$ есть свой счетчик $$$c(v)$$$.

Первоначально в вершине $$$s$$$ расположена фишка, и все счетчики, кроме $$$c(s)$$$, равны $$$0$$$; $$$c(s)$$$ равен $$$1$$$.

Ваша задача — переместить фишку в вершину $$$t$$$. Для этого вы можете совершить следующую последовательность шагов. Пусть сейчас фишка расположена в вершине $$$v$$$. За один шаг вы можете сделать следующее:

  1. выбрать одну из соседних вершин $$$to$$$ вершины $$$v$$$ равновероятно ($$$to$$$ является соседней вершиной $$$v$$$ тогда и только тогда, когда в дереве есть ребро $$$\{v, to\}$$$);
  2. передвинуть фишку в вершину $$$to$$$ и увеличить $$$c(to)$$$ на $$$1$$$.

Вы будете повторять данную операцию, пока не достигните вершины $$$t$$$.

Для каждой вершины $$$v$$$ вычислите математическое ожидание значения $$$c(v)$$$ по модулю $$$998\,244\,353$$$.

Входные данные

В первой строке заданы три целых числа: $$$n$$$, $$$s$$$ и $$$t$$$ ($$$2 \le n \le 2 \cdot 10^5$$$; $$$1 \le s, t \le n$$$; $$$s \neq t$$$) — количество вершин в дереве, стартовая и конечная вершины.

В следующих $$$n - 1$$$ строках заданы ребра дерева: по одному в строке. В $$$i$$$-й строке заданы два целых числа $$$u_i$$$ и $$$v_i$$$ ($$$1 \le u_i, v_i \le n$$$; $$$u_i \neq v_i$$$), обозначающих ребро между вершинами $$$u_i$$$ и $$$v_i$$$.

Гарантируется, что заданные ребра образуют дерево.

Выходные данные

Выведите $$$n$$$ чисел: математические ожидания значений $$$c(v)$$$ по модулю $$$998\,244\,353$$$ для каждого $$$v$$$ от $$$1$$$ по $$$n$$$.

Формально, пусть $$$M = 998\,244\,353$$$. Можно показать, что ответ может быть представлен в виде несократимой дроби $$$\frac{p}{q}$$$, где $$$p$$$ и $$$q$$$ — целые числа, и $$$q \not \equiv 0 \pmod{M}$$$. Выведите целое число, равное $$$p \cdot q^{-1} \bmod M$$$. Другими словами, выведите такое целое число $$$x$$$, что $$$0 \le x < M$$$ и $$$x \cdot q \equiv p \pmod{M}$$$.

Примеры
Входные данные
3 1 3
1 2
2 3
Выходные данные
2 2 1
Входные данные
4 1 3
1 2
2 3
1 4
Выходные данные
4 2 1 2
Входные данные
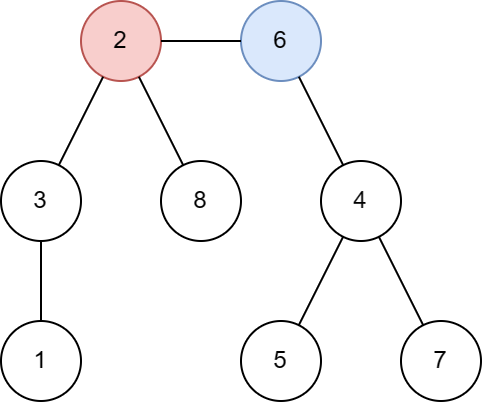
8 2 6
6 4
6 2
5 4
3 1
2 3
7 4
8 2
Выходные данные
1 3 2 0 0 1 0 1
Примечание

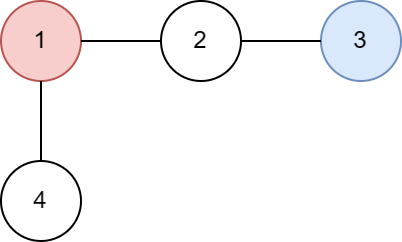
Дерево из первого примера показано ниже:

Посчитаем математическое ожидание $$$E[c(1)]$$$:
  • $$$P(c(1) = 0) = 0$$$, так как $$$c(1)$$$ изначально равно $$$1$$$.
  • $$$P(c(1) = 1) = \frac{1}{2}$$$, так как есть только одна последовательность шагов, приводящая к $$$c(1) = 1$$$. Это $$$1 \rightarrow 2 \rightarrow 3$$$ с вероятностью $$$1 \cdot \frac{1}{2}$$$.
  • $$$P(c(1) = 2) = \frac{1}{4}$$$: единственный путь $$$1 \rightarrow_{1} 2 \rightarrow_{0.5} 1 \rightarrow_{1} 2 \rightarrow_{0.5} 3$$$.
  • $$$P(c(1) = 3) = \frac{1}{8}$$$: единственный путь $$$1 \rightarrow_{1} 2 \rightarrow_{0.5} 1 \rightarrow_{1} 2 \rightarrow_{0.5} 1 \rightarrow_{1} 2 \rightarrow_{0.5} 3$$$.
  • $$$P(c(1) = i) = \frac{1}{2^i}$$$ в общем случае.
В результате $$$E[c(1)] = \sum\limits_{i=1}^{\infty}{i \frac{1}{2^i}} = 2$$$.
Изображение дерева во втором тесте
Изображение дерева в третьем тесте