| Codeforces Round 870 (Div. 2) |
|---|
| Закончено |
Это интерактивная задача.
Есть $$$n$$$ различных загаданных точек с вещественными координатами на двухмерной евклидовой плоскости. За один запрос вы можете спросить прямую $$$ax + by + c = 0$$$ и получить в ответ проекции всех $$$n$$$ точек на эту прямую в некотором порядке. Выводимые проекции могут быть неточными, прочтите секцию протокола взаимодействия для лучшего понимания.
Используя минимальное число запросов, найдите все $$$n$$$ точек и выведите их в некотором порядке. Под минимальностью понимается минимальное число запросов, необходимое для решения любого набора входных данных из $$$n$$$ точек.
Загаданные точки определяются заранее и не меняются во время взаимодействия. Другими словами, интерактор не адаптивен.
Проекцией точки $$$A$$$ на прямую $$$ax + by + c = 0$$$ является точка на прямой, ближайшая к $$$A$$$.
В первой строке находится единственное целое число $$$t$$$ ($$$1 \leq t \leq 50$$$) — число наборов входных данных.
Далее следуют наборы входных данных.
В первой строке набора входных данных находится единственное целое число $$$n$$$ ($$$2 \leq n \leq 25$$$) — число загаданных точек.
Для каждого набора входных данных гарантируется, что для любых двух загаданных точек их $$$x$$$ координаты отличаются хотя бы на $$$1$$$. Аналогично, $$$y$$$ координаты любых двух точек отличаются хотя бы на $$$1$$$.
Координаты $$$x$$$ и $$$y$$$ всех скрытых точек не превышают $$$100$$$ по абсолютному значению.
Чтобы запросить прямую $$$ax + by + c = 0$$$, выведите «? a b c», где все a, b и c — вещественные числа до $$$100$$$ по абсолютному значению. Для меньшей потери точности числа $$$a$$$ и $$$b$$$ должны удовлетворять условию $$$|a| + |b| \geq 0.1$$$, где $$$|a|$$$ — модуль числа $$$a$$$.
В качестве ответа на запрос вы получите $$$n$$$ точек в формате «x_1 y_1 ... x_n y_n», где точки $$$(x_i, y_i)$$$ являются проекциями загаданных точек на прямую $$$ax + by + c = 0$$$ в некотором порядке. Гарантируется, что каждая выведенная точка находится на расстоянии не более $$$10^{-4}$$$ от точной точки проекции. Каждая координата выводится с не более чем 9 знаками после запятой.
Смотрите пример взаимодействия для лучшего понимания.
Если вы сделаете слишком много запросов, то получите вердикт Wrong answer.
Чтобы вывести ответ, вы должны вывести «! x_1 y_1 ... x_n y_n», где $$$(x_i, y_i)$$$ — координаты загаданных точек. Загаданные точки можно выводить в любом порядке. Ответ будет считаться корректным, если каждая из выведенных точек будет на расстоянии не более $$$10^{-3}$$$ от соответствующей загаданной. Вывод ответа не считается за запрос.
После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте:
- fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Взломы
Для того чтобы сделать взлом, используйте следующий формат теста.
В первой строке выведите одно целое число $$$t$$$ ($$$1 \leq t \leq 50$$$) — число наборов входных данных.
Далее идет описание наборов входных данных.
В первой строке для набора входных данных выведите одно целое число $$$n$$$ ($$$2 \leq n \leq 25$$$). В следующих $$$n$$$ строках выведите по 2 числа. Числа в $$$i$$$-й строке должны соответствовать числам $$$x_i$$$ и $$$y_i$$$ соответственно. Выведенные точки должны удовлетворять условиям описанным в секции ввода.
1 2 1 1 2.5 1 1.500000001 1.500000000 2 2
? 0 1 -1 ? 0.2 -0.2 0 ! 1 3 2.5 0.500000001
В примере загаданные точки $$$(1, 3)$$$ и $$$(2.5, 0.5)$$$
Рисунок, объясняющий первый запрос:
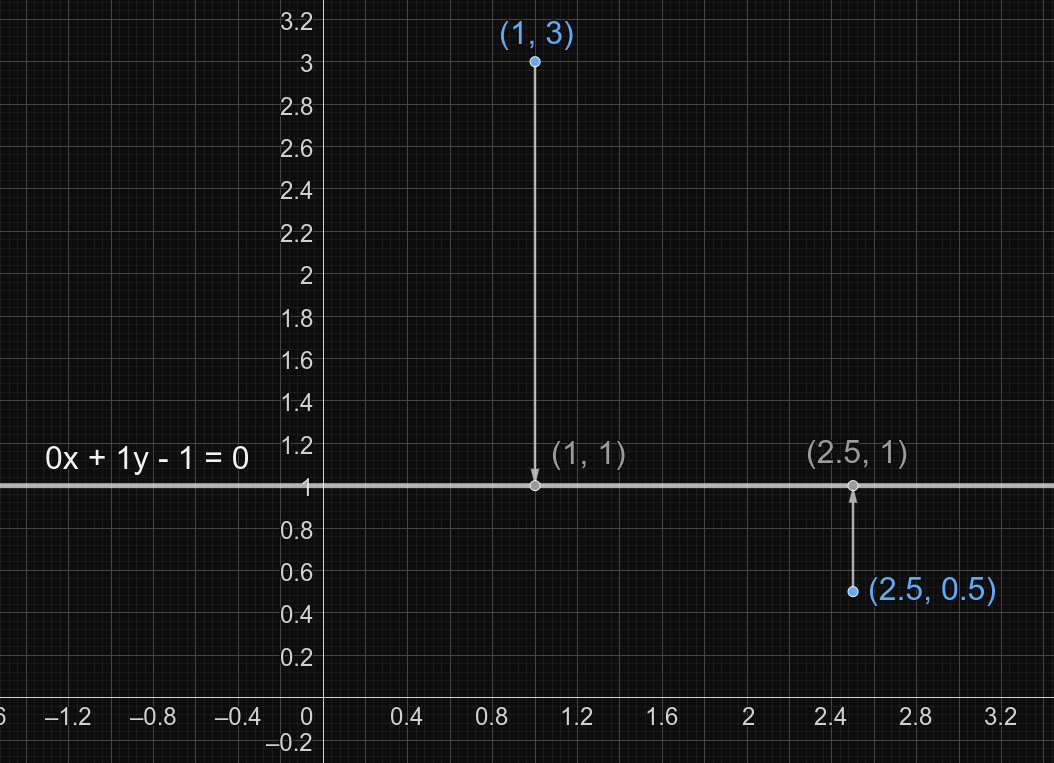
Рисунок, объясняющий второй запрос:
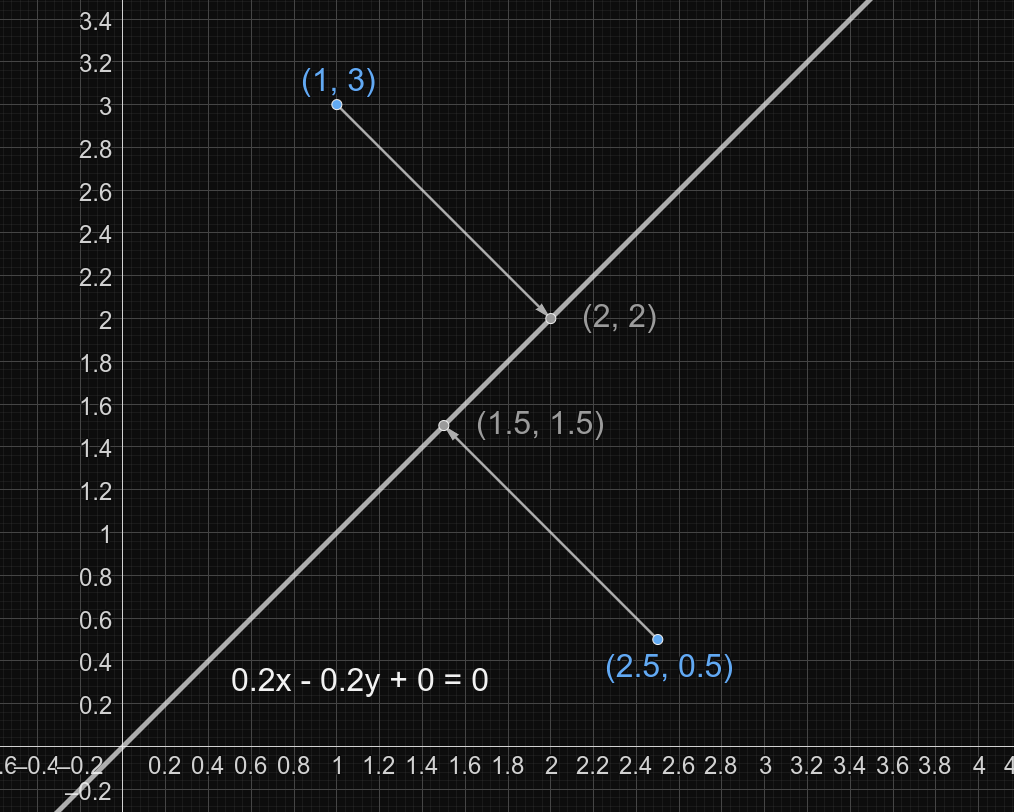
| Название |
|---|




