| Чемпионат КРОК 2012 - Финал |
|---|
| Закончено |
Задан ориентированный граф G с n вершинами и m дугами (кратные дуги и петли разрешаются). Требуется покрасить каждую вершину этого графа в один из k (k ≤ n) цветов таким образом, что для любой дуги графа ведущей из вершины u в вершину v верно, что вершина v покрашена в следующий цвет по сравнению с цветом вершины u.
Считайте, что цвета пронумерованы по циклу от 1 до k. Это означает, что для каждого цвета i (i < k) следующим является цвет i + 1, следующим для цвета k является цвет 1. Обратите внимание, что если k = 1, то цвет 1 следующий для самого себя.
Ваша задача — найти и вывести максимальное число k (k ≤ n) такое, что орграф G можно покрасить в k цветов описанным выше способом. Обратите внимание, что вы не обязаны использовать все k цветов для покраски вершин (то есть, для каждого цвета i не обязательно должна существовать вершина покрашенная в цвет i).
Первая строка входных данных содержит два целых числа n и m (1 ≤ n, m ≤ 105), разделенных пробелом — количество вершин и дуг орграфа G, соответственно.
Следующие m строк содержат по два целых числа ai и bi (1 ≤ ai, bi ≤ n), разделенных пробелом, которые означают, что дуга номер i ведет из вершины номер ai в вершину номер bi.
Допустимы кратные дуги и петли.
Выведите единственное целое число — максимальное возможное количество цветов в покраске (то есть, значение k, описанное в условии). Обратите внимание, что искомое значение k должно удовлетворять неравенству 1 ≤ k ≤ n.
4 4
1 2
2 1
3 4
4 3
2
5 2
1 4
2 5
5
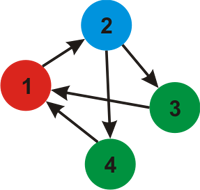
4 5
1 2
2 3
3 1
2 4
4 1
3
4 4
1 1
1 2
2 1
1 2
1
Для первого примера, k = 2, картинка ниже изображает два цвета (стрелочки показывают какой цвет, для какого следующий).

С k = 2 один из возможных способов раскрасить граф изображен ниже.
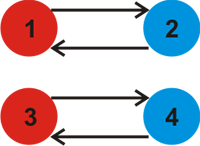
Можно доказать, что большее значение k выбрать невозможно.
Для второго примера, ниже приведена картинка для k = 5 цветов.
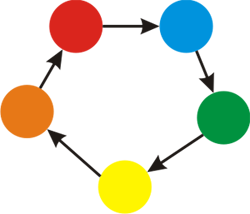
Возможная раскраска графа изображена ниже:
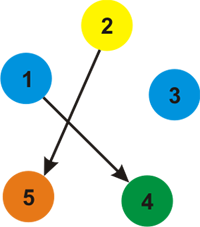
Для третьего примера, ниже приведена картинка для k = 3 цветов.
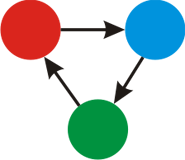
Возможная раскраска графа изображена ниже:
| Название |
|---|




