| Codeforces Round 875 (Div. 1) |
|---|
| Закончено |
Copil Copac получил список из $$$n-1$$$ ребра, описывающих дерево на $$$n$$$ вершинах. Он решил нарисовать его, используя следующий алгоритм:
- Шаг $$$0$$$: Рисует первую вершину (вершину $$$1$$$). Переходит к шагу $$$1$$$.
- Шаг $$$1$$$: Для каждого ребра из входных данных в порядке ввода: если ребро соединяет уже нарисованную вершину $$$u$$$ с не нарисованной вершиной $$$v$$$, он рисует $$$v$$$ и ребро. После прохода по всем рёбрам он переходит к шагу $$$2$$$.
- Шаг $$$2$$$: Если все вершины нарисованы, завершает алгоритм. Иначе переходит к шагу $$$1$$$.
Количество проходов определяется как количество раз, которое Copil Copac выполняет шаг $$$1$$$.
Найдите количество проходов, необходимых Copil Copac для рисования дерева.
Каждый тест содержит несколько наборов входных данных. В первой строке находится одно целое число $$$t$$$ ($$$1 \leq t \leq 10^4$$$) — количество наборов входных данных. Затем следует описание наборов.
Первая строка каждого набора содержит одно целое число $$$n$$$ ($$$2 \le n \le 2 \cdot 10^5$$$) — количество вершин дерева.
Следующие $$$n - 1$$$ строк каждого набора содержат по два целых числа $$$u_i$$$ и $$$v_i$$$ ($$$1 \le u_i, v_i \le n$$$, $$$u_i \neq v_i$$$) — концы ребра $$$(u_i,v_i)$$$, которое является $$$i$$$-м ребром в списке. Гарантируется, что заданные ребра образуют дерево.
Гарантируется, что сумма $$$n$$$ по всем наборам входных не превышает $$$2 \cdot 10^5$$$.
Для каждого набора входных данных выведите количество проходов, необходимых Copil Copac для рисования дерева.
264 51 31 23 41 675 62 42 71 31 24 5
2 3
В первом наборе входных данных:
После первого прохода дерево будет выглядеть так:
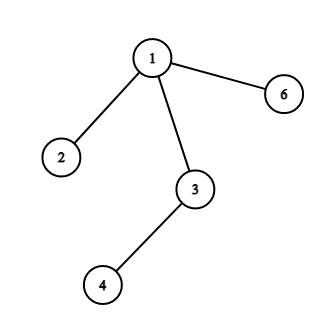
После второго прохода:
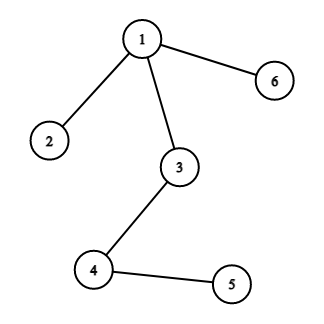
Таким образом, Copil Copac нужно $$$2$$$ прохода, чтобы нарисовать дерево.
| Название |
|---|




