На двумерной плоскости имеется $$$n$$$ попарно различных точек и прямая $$$x+y=k$$$. Точка $$$i$$$ находится в точке $$$(x_i,y_i)$$$. Все точки имеют неотрицательные координаты и находятся строго под прямой. Другими словами, $$$0 \leq x_i,y_i, x_i+y_i < k$$$.
Тенцинг хочет стереть все точки. Он может выполнить следующие две операции:
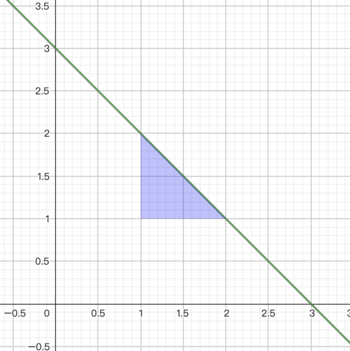
- Нарисовать треугольник: Тенцинг выберет два неотрицательных целых числа $$$a$$$, $$$b$$$, которые удовлетворяют условию $$$a+b<k$$$, тогда все точки внутри треугольника, образованного прямыми $$$x=a$$$, $$$y=b$$$ и $$$x+y=k$$$ будут стерты. Можно показать, что этот треугольник является равнобедренным прямоугольным треугольником. Пусть длины сторон треугольника равны $$$l$$$, $$$l$$$ и $$$\sqrt 2 l$$$ соответственно. Тогда стоимость этой операции равна $$$l \cdot A$$$.
Синяя область следующего рисунка описывает треугольник с $$$a=1,b=1$$$ со стоимостью $$$=1\cdot A$$$.
- Стереть определенную точку: Тенцинг выбирает целое число $$$i$$$, которое удовлетворяет условию $$$1 \leq i \leq n$$$ и стирает точку $$$i$$$. Стоимость этой операции равна $$$c_i$$$.
Помогите Тенцингу найти минимальную стоимость стирания всех точек.
Первая строка содержит три целых числа $$$n$$$, $$$k$$$ и $$$A$$$ ($$$1\leq n,k\leq 2\cdot 10^5$$$, $$$1\leq A\leq 10^4$$$) — количество точек, коэффициент, описывающий гипотенузу треугольника и коэффициент, описывающий стоимость построения треугольника.
В следующих $$$n$$$ строках входных данных $$$i$$$-я строка содержит три целых числа $$$x_i,y_i,c_i$$$ ($$$0\leq x_i,y_i,x_i+y_i< k$$$, $$$1\leq c_i\leq 10^4$$$) — координаты $$$i$$$-й точки и стоимость ее стирания с помощью второй операции. Гарантируется, что координаты попарно различны.
Выведите одно целое число –минимальную стоимость стирания всех точек.
4 6 1 1 2 1 2 1 1 1 1 1 3 2 6
4
6 7 1 4 2 1 3 3 1 5 1 4 3 2 5 4 1 1 0 6 4
4
10 4 100 0 0 1 0 1 1 0 2 50 0 3 200 1 0 1 1 1 1 1 2 1 2 0 200 2 1 200 3 0 200
355
Рисунок первого примера:
Тенцинг выполняет следующие операции:
- построить треугольник с $$$a=3,b=2$$$, стоимость $$$=1\cdot A=1$$$.
- стереть первую точку, стоимость $$$=1$$$.
- стереть вторую точку, стоимость $$$=1$$$.
- стереть третью точку, стоимость $$$=1$$$.
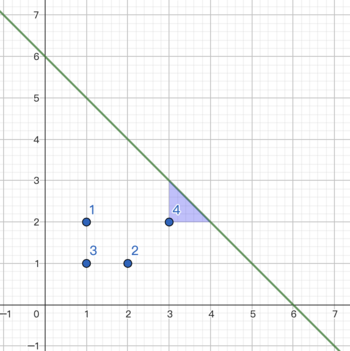
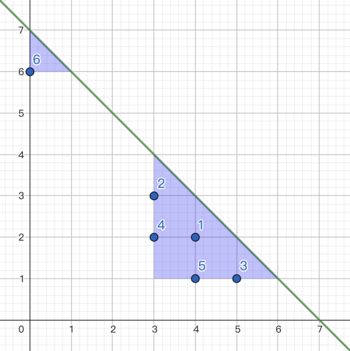
Рисунок для второго примера:
| Название |
|---|




