| Codeforces Round 881 (Div. 3) |
|---|
| Закончено |
Ване очень нравится математика. Однажды, когда он решал очередную задачу по математике, он придумал интересное дерево. Это дерево строится следующим образом.
Изначально в дереве есть только одна вершина с номером $$$1$$$ — корень дерева. Затем, Ваня добавляет к ней двух детей, присваивая им последовательные номера — $$$2$$$ и $$$3$$$ соответственно. После этого, он будет добавлять детей к вершинам по возрастанию их номеров, начиная с $$$2$$$, присваивая их детям минимальные не занятые номера. В итоге, у Вани получится бесконечное дерево с корнем в вершине $$$1$$$, где каждая вершина будет иметь ровно два ребенка, а номера вершин будут расположены последовательно по слоям.
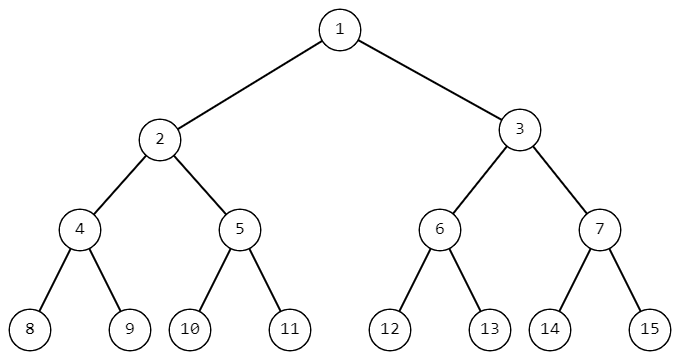 Часть дерева Вани.
Часть дерева Вани. Ване стало интересно, чему равна сумма номеров вершин на пути от вершины с номером $$$1$$$ до вершины с номером $$$n$$$ в таком дереве. Так как Ваня не любит считать, он попросил Вас помочь ему узнать эту сумму.
Первая строка входных данных содержит одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных.
Далее следует $$$t$$$ строк — описание наборов входных данных. Каждая строка содержит одно целое число $$$n$$$ ($$$1 \le n \le 10^{16}$$$) — номер вершины, для которой Ваня хочет посчитать сумму номеров вершин на пути от корня до этой вершины.
Для каждого набора входных данных выведите одно целое число — искомую сумму.
63103711000000000000000015
4 18 71 1 19999999999999980 26
В первом наборе данных примера на пути от корня до вершины $$$3$$$ лежат две вершины $$$1$$$ и $$$3$$$, для них сумма равна $$$4$$$.
Во втором наборе данных примера на пути от корня до вершины с номером $$$10$$$ лежат вершины $$$1$$$, $$$2$$$, $$$5$$$, $$$10$$$, сумма их номеров равна $$$1+2+5+10 = 18$$$.
| Название |
|---|




