| Codeforces Round 881 (Div. 3) |
|---|
| Закончено |
У Тимофея в саду растёт яблоня, она представляет собой корневое дерево из $$$n$$$ вершин с корнем в вершине $$$1$$$ (вершины пронумерованы от $$$1$$$ от $$$n$$$). Деревом называется связный граф без циклов, петель и кратных ребер.
Это дерево очень необычное — оно растёт корнем вверх. Впрочем, в этом нет ничего необычного для деревьев в программировании.
Яблоня достаточно молодая, поэтому на ней вырастет всего два яблока. Яблоки вырастут в определённых вершинах (эти вершины могу совпадать). После того как яблоки вырастут, Тимофей начнёт трясти яблоню, пока яблоки не упадут. Каждый раз, когда Тимофей трясёт яблоню, с каждым из яблок происходит следующее:
Пусть яблоко сейчас находится в вершине $$$u$$$.
- Если у вершины $$$u$$$ есть ребёнок, то яблоко перемещается в него (если таких вершин несколько, то яблоко может переместиться в любую из них).
- Иначе яблоко падает с дерева.
Можно показать, что через конечное время оба яблока упадут с дерева.
У Тимофея есть $$$q$$$ предположений, в каких вершинах могут вырасти яблоки. Он предполагает, что яблоки могут вырасти в вершинах $$$x$$$ и $$$y$$$, и хочет узнать количество пар вершин ($$$a$$$, $$$b$$$), с которых яблоки могут упасть с дерева, где $$$a$$$ — вершина, с которой упадёт яблоко из вершины $$$x$$$, $$$b$$$ — вершина, с которой упадёт яблоко из вершины $$$y$$$. Помогите ему это сделать.
В первой строке дано число $$$t$$$ ($$$1 \leq t \leq 10^4$$$) — количество наборов входных данных.
В первой строке каждого набора входных данных даны числа $$$n$$$ ($$$2 \leq n \leq 2 \cdot 10^5$$$) — количество вершин в яблоне.
Далее следует $$$n - 1$$$ строка, описывающая дерево. В $$$i$$$-й из них даны числа $$$u_i$$$ и $$$v_i$$$ ($$$1 \leq u_i, v_i \leq n$$$, $$$u_i \ne v_i$$$) — ребро в дереве.
В следующей строке дано единственное целое число $$$q$$$ ($$$1 \leq q \leq 2 \cdot 10^5$$$) — количество предположений Тимофея.
Далее следует $$$q$$$ строк, описывающих предположения Тимофея. В $$$i$$$-й строке даны числа $$$x_i$$$ и $$$y_i$$$ ($$$1 \leq x_i, y_i \leq n$$$) — предполагаемые вершины, на которых вырастут яблоки.
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превышает $$$2 \cdot 10^5$$$. Аналогично, сумма $$$q$$$ по всем наборам входных данных не превышает $$$2 \cdot 10^5$$$.
Для каждого запроса Тимофея выведите количество упорядоченных пар вершин, с которых яблоки могут упасть с дерева, если предположение окажется верным, в отдельной строке.
251 23 45 33 243 45 14 41 331 21 331 12 33 1
2 2 1 4 4 1 2
255 11 22 34 325 55 153 25 32 14 234 32 14 2
1 2 1 4 2
В первом примере:
- Для первого запроса существует две возможные пары вершин, с которых яблоки могут упасть: $$$(4, 4), (5, 4)$$$.
- Для второго запроса также существует две пары: $$$(5, 4), (5, 5)$$$.
- Для третьего запроса есть всего одна пара: $$$(4, 4)$$$.
- Для четвертого запроса существует $$$4$$$ пары: $$$(4, 4), (4, 5), (5, 4), (5, 5)$$$.
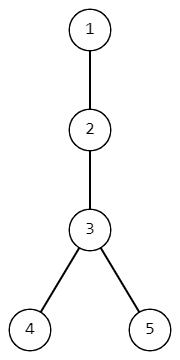 Дерево из первого примера.
Дерево из первого примера. Во втором примере для первого предположения есть $$$4$$$ возможных пар вершин, с которых могут упасть яблоки: $$$(2, 3), (2, 2), (3, 2), (3, 3)$$$. Для второго запроса есть всего одна возможная пара: $$$(2, 3)$$$. Для третьего запроса есть две пары: $$$(3, 2), (3, 3)$$$.
| Название |
|---|




