| Codeforces Round 884 (Div. 1 + Div. 2) |
|---|
| Закончено |
Дано дерево на $$$n$$$ вершинах, пронумерованных числами $$$1,2,\dots,n$$$. $$$i$$$-е ребро соединяет вершины $$$u_i$$$ и $$$v_i$$$ и имеет некоторый неизвестный целый положительный вес $$$w_i$$$. Вам также известны расстояния $$$d_i$$$ между вершинами $$$i$$$ и $$$i+1$$$ для всех $$$1 \le i \le n-1$$$ (это расстояние равно сумме весов рёбер на простом пути между вершинами дерева $$$i$$$ и $$$i+1$$$).
Найдите вес каждого ребра. Если существует несколько решений, выведите любое из них. Если не существует весов $$$w_i$$$, согласующихся со всеми данными, выведите одно целое число $$$-1$$$.
Первая строка содержит целое число $$$n$$$ ($$$2 \le n \le 10^5$$$).
В $$$i$$$-й из следующих $$$n-1$$$ строк содержатся по два числа: $$$u_i$$$ и $$$v_i$$$ ($$$1 \le u_i,v_i \le n$$$, $$$u_i \ne v_i$$$).
В последней строке содержится $$$n-1$$$ целых чисел $$$d_1,\dots,d_{n-1}$$$ ($$$1 \le d_i \le 10^{12}$$$).
Гарантируется, что заданные ребра образуют дерево.
Если решения не существует, выведите одно целое число $$$-1$$$. В противном случае выведите $$$n-1$$$ строку, содержащую веса $$$w_1,\dots,w_{n-1}$$$.
Если существует несколько решений, выведите любое из них.
5 1 2 1 3 2 4 2 5 31 41 59 26
31 10 18 8
3 1 2 1 3 18 18
-1
9 3 1 4 1 5 9 2 6 5 3 5 8 9 7 9 2 236 205 72 125 178 216 214 117
31 41 59 26 53 58 97 93
В первом примере дерево выглядит следующим образом:
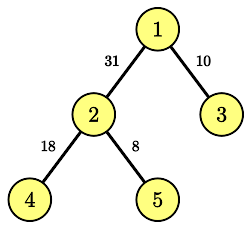
Во втором примере вес $$$w_2$$$ не может быть равен $$$0$$$, поскольку должен быть целым положительным числом. Поэтому решения нет.
В третьем примере дерево выглядит следующим образом:
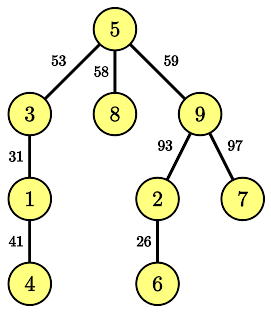
| Название |
|---|




