| Codeforces Round 891 (Div. 3) |
|---|
| Закончено |
Даны два массива $$$a$$$ и $$$b$$$, оба длины $$$n$$$. Элементы обоих массивов пронумерованы от $$$1$$$ до $$$n$$$. Вы строите ориентированный граф, где существует ориентированное ребро из $$$u$$$ в $$$v$$$ ($$$u\neq v$$$), если $$$a_u-a_v \ge b_u-b_v$$$.
Вершина $$$V$$$ называется сильной, если существует путь от $$$V$$$ ко всем остальным вершинам.
Путем в ориентированном графе называют такую цепочку из нескольких вершин, соединенных рёбрами, что двигаясь от вершины $$$u$$$ по направлениям рёбер можно достичь вершины $$$v$$$.
Ваша задача — найти все сильные вершины.
Например, если $$$a=[3,1,2,4]$$$ и $$$b=[4,3,2,1]$$$, граф будет выглядеть так:
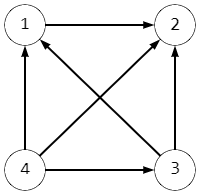 Граф имеет только одну сильную вершину с номером $$$4$$$
Граф имеет только одну сильную вершину с номером $$$4$$$ Первая строка содержит целое число $$$t$$$ ($$$1\le t\le 10^4$$$) — количество наборов входных данных.
Первая строка каждого набора содержит целое число $$$n$$$ ($$$2 \le n \le 2\cdot 10^5$$$) — длину $$$a$$$ и $$$b$$$.
Вторая строка содержит $$$n$$$ целых чисел $$$a_1,a_2 \dots a_n$$$ ($$$-10^9 \le a_i \le 10^9$$$) — массив $$$a$$$.
Третья строка содержит $$$n$$$ целых чисел $$$b_1,b_2 \dots b_n$$$ ($$$-10^9 \le b_i \le 10^9$$$) — массив $$$b$$$.
Гарантируется, что сумма значений $$$n$$$ по всем наборам входных данных не превышает $$$2\cdot 10^5$$$.
Для каждого набора входных данных выведите две строки: в первой строке выведите количество сильных вершин, а во второй строке выведите все сильные вершины в возрастающем порядке.
543 1 2 44 3 2 151 2 4 1 25 2 3 3 121 22 130 2 11 3 235 7 4-2 -3 -6
1 4 2 3 5 1 2 3 1 2 3 2 2 3
Первый пример разобран в условии.
Для второго примера граф выглядит так:
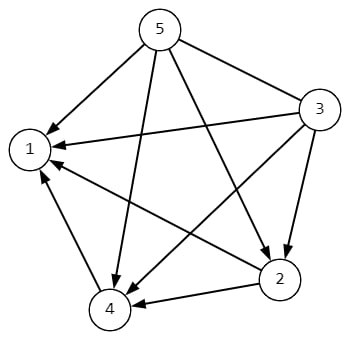 Граф имеет две сильные вершины с номерами в $$$3$$$ и $$$5$$$. Обратите внимание, что между вершинами $$$3$$$ и $$$5$$$ проведено двунаправленное ребро.
Граф имеет две сильные вершины с номерами в $$$3$$$ и $$$5$$$. Обратите внимание, что между вершинами $$$3$$$ и $$$5$$$ проведено двунаправленное ребро. В третьем примере вершины соединяет единственное направленное ребро от вершины $$$2$$$ к вершине $$$1$$$, поэтому единственная сильная вершина это $$$2$$$.
В четвертом примере все вершины попарно соединены двунаправленными рёбрами, поэтому от каждой вершины есть путь к любой другой.
| Название |
|---|




