С таким названием задача точно не может быть задачей на графы...
У Чанеки есть граф с $$$n$$$ вершинами и $$$n-1$$$ ребрами. Некоторые ребра являются направленными, а некоторые — неориентированными. Ребро $$$i$$$ соединяет вершину $$$u_i$$$ с вершиной $$$v_i$$$. Если $$$t_i=0$$$, то ребро $$$i$$$ является ненаправленным. Если $$$t_i=1$$$, то ребро $$$i$$$ направлено в сторону от $$$u_i$$$ к $$$v_i$$$. Известно, что если сделать все ребра ненаправленными, то граф превратится в дерево$$$^\dagger$$$.
Чанека хочет направить все ненаправленные ребра и раскрасить каждое ребро (разные ребра могут иметь один и тот же цвет).
После этого, предположим, что Чанека начинает прогулку из произвольной вершины $$$x$$$ в произвольную вершину $$$y$$$ (возможно, что $$$x=y$$$), проходя через одно или несколько ребер. Ей разрешается проходить через каждое ребро, следуя направлению ребра или в противоположную от направления сторону. Также ей разрешается посещать вершину или ребро более одного раза. Во время прогулки Чанека хранит стек шаров, который изначально пуст до начала прогулки. Каждый раз, когда Чанека проходит через ребро, она делает следующее:
- Если Чанека проходит его в правильном направлении, она кладет на вершину стека новый шар, цвет которого совпадает с цветом ребра.
- Если Чанека проходит по нему в обратном направлении, то она убирает шар, находящийся на вершине стека.
Прогулка называется стековой тогда и только тогда, когда стек не пуст перед каждым проходом Чанеки по ребру в обратном направлении.
Прогулка называется шаро-стековой тогда и только тогда, когда она стековая и каждый раз, когда Чанека проходит через ребро в обратном направлении, цвет шарика, вынутого из стека, совпадает с цветом пройденного ребра.
Можно ли направить все неориентированные ребра и раскрасить все рёбра так, чтобы все стековые прогулки были также шаро-стековыми? Если это возможно, то найдите пример, в котором используется максимальное количество различных цветов среди всех допустимых способов направления и раскраски. Если таких решений несколько, выведите любое из них.
$$$^\dagger$$$ Дерево — это связный граф, не имеющий циклов.
Первая строка содержит одно целое число $$$n$$$ ($$$2\leq n\leq10^5$$$) — количество вершин в графе.
В $$$i$$$-й из следующих $$$n-1$$$ строк содержится три целых числа $$$u_i$$$, $$$v_i$$$ и $$$t_i$$$ ($$$1 \leq u_i,v_i \leq n$$$; $$$0\leq t_i\leq1$$$) — ненаправленное ребро, соединяющее вершины $$$u_i$$$ и $$$v_i$$$, если $$$t_i=0$$$, или направленное ребро из вершины $$$u_i$$$ в вершину $$$v_i$$$, если $$$t_i=1$$$. Если сделать все ребра ненаправленными, то граф станет деревом.
Выведите одно число $$$-1$$$, если искомой конструкции не существует.
В противном случае вывод состоит из $$$n$$$ строк, описывающих вашу конструкцию. Первая строка содержит целое число $$$z$$$, равное количеству используемых цветов. В $$$i$$$-й из следующих $$$n-1$$$ строк содержится три целых числа $$$p$$$, $$$q$$$ и $$$c$$$ ($$$1\leq p,q\leq n$$$; $$$1\leq c\leq z$$$) — ребро, соединяющее вершины $$$p$$$ и $$$q$$$ в графе, направлено от вершины $$$p$$$ к вершине $$$q$$$ и окрашено в цвет $$$c$$$. Если таких решений несколько, выведите любое из них.
Обратите внимание, что поскольку в вашей конструкции должно быть $$$z$$$ различных цветов, это означает, что каждый цвет от $$$1$$$ до $$$z$$$ должен встречаться в графе хотя бы один раз.
5 2 5 1 1 3 0 5 4 0 1 5 1
3 1 5 2 5 4 1 2 5 2 3 1 3
Ниже приведен заданный граф.
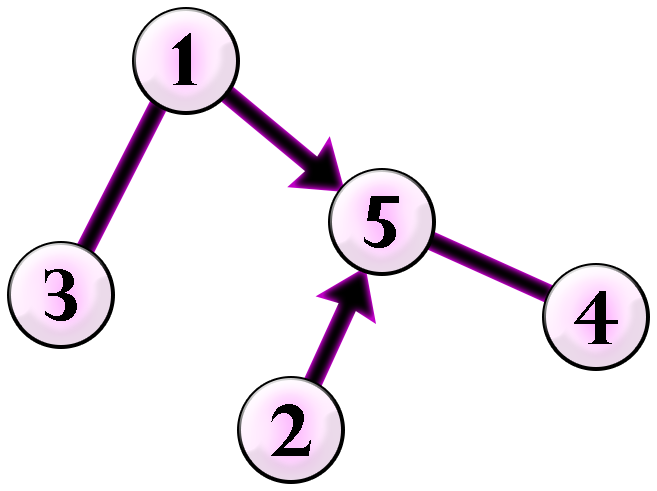
Чанека может направить все неориентированные ребра и раскрасить каждое ребро следующим образом:
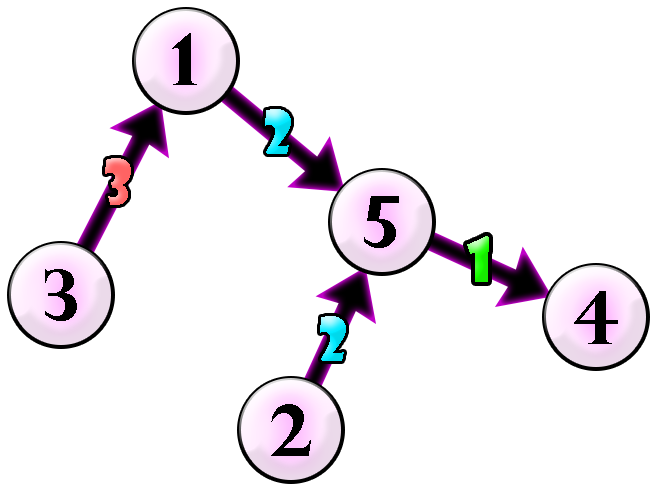
В качестве примера рассмотрим путь $$$3→1→5→2→5→4→5$$$. Покажем, что этот путь является шаро-стековым.
- Чанека начинается в вершине $$$3$$$. Стеком является $$$[]$$$.
- Чанека переходит в вершину $$$1$$$. Она кладет шар цвета $$$3$$$. В стеке $$$[3]$$$.
- Чанека перемещается в вершину $$$5$$$. Она кладет шар цвета $$$2$$$. В стеке $$$[3,2]$$$.
- Чанека перемещается в вершину $$$2$$$. Она убирает шар цвета $$$2$$$ (того же цвета, что и ребро). В стеке оказывается $$$[3]$$$.
- Чанека перемещается в вершину $$$5$$$. Она кладет шар цвета $$$2$$$. В стеке $$$[3,2]$$$.
- Чанека перемещается в вершину $$$4$$$. Она кладет шар цвета $$$1$$$. В стеке $$$[3,2,1]$$$.
- Чанека перемещается в вершину $$$5$$$. Она убирает шар цвета $$$1$$$ (того же цвета, что и ребро). В стеке оказывается $$$[3,2]$$$.
Поскольку каждый раз, когда Чанека снимает шар со стека, он имеет тот же цвет, что и пройденное ребро, то вышеописанная прогулка является шаро-стековой. Можно показать, что если мы направим и раскрасим ребра так, как показано выше, то любая возможная стековая прогулка будет также шаро-стековой.
| Название |
|---|




