У вас есть доска размером $$$n \times n$$$ ($$$n$$$ строк и $$$n$$$ столбцов) и два массива положительных целых чисел $$$a$$$ и $$$b$$$ размера $$$n$$$.
Ваша задача — разместить фишки на этой доске таким образом, чтобы для каждой клетки $$$(i, j)$$$ выполнялось следующее условие:
- есть хотя бы одна клетка с фишкой либо в том же столбце, либо в той же строке, что и $$$(i, j)$$$. Иными словами, существует такая клетка с фишкой $$$(x, y)$$$, что $$$x = i$$$ или $$$y = j$$$ (или выполняются оба условия).
Стоимость размещения фишки в клетке $$$(i, j)$$$ равна $$$a_i + b_j$$$.
Например, для $$$n=3$$$, $$$a=[1, 4, 1]$$$ и $$$b=[3, 2, 2]$$$ один из способов расставить фишки следующий:
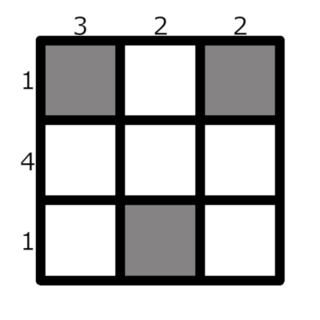Свободные клетки обозначены белым цветом Суммарная стоимость для такого размещения равна $$$(1+3) + (1+2) + (1+2) = 10$$$.
Вычислите минимально возможную суммарную стоимость размещения фишек в соответствии с вышеописанными правилами.
Первая строка содержит одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных.
Первая строка каждого теста содержит одно целое число $$$n$$$ ($$$1 \le n \le 3 \cdot 10^5$$$).
Вторая строка содержит $$$n$$$ целых чисел $$$a_1, a_2, \dots, a_n$$$ ($$$1 \le a_i \le 10^9$$$).
Третья строка содержит $$$n$$$ целых чисел $$$b_1, b_2, \dots, b_n$$$ ($$$1 \le b_i \le 10^9$$$).
Сумма $$$n$$$ по всем наборам входных данных не превышает $$$3 \cdot 10^5$$$.
Для каждого набора входных данных выведите одно целое число — минимально возможную суммарную стоимость размещения фишек в соответствии с правилами.
431 4 13 2 214524 52 355 2 4 5 33 4 2 1 5
10 9 13 24
Первый набор входных данных примера разобран в условии.
