Монокарп пытается добраться домой с работы. В данный момент он находится в точке $$$O = (0, 0)$$$ двумерной координатной плоскости; его дом находится в точке $$$P = (P_x, P_y)$$$.
К сожалению, уже поздний вечер, и поэтому очень темно. Монокарп боится темноты. Он хотел бы идти домой по освещенному пути.
К счастью, есть два фонаря, расположенные в точках $$$A = (A_x, A_y)$$$ и $$$B = (B_x, B_y)$$$. Вы можете выбрать любое неотрицательное число $$$w$$$ и установить мощность обоих фонарей равной $$$w$$$. Если мощность фонаря установлена на $$$w$$$, то он освещает круг радиусом $$$w$$$ с центром в месте расположения фонаря (включая границы круга).
Вам нужно выбрать минимальное неотрицательное значение $$$w$$$ для мощности фонарей таким образом, чтобы существовал полностью освещенный путь от точки $$$O$$$ до точки $$$P$$$. Считайте, что фонари не мешают движению Монокарпа.
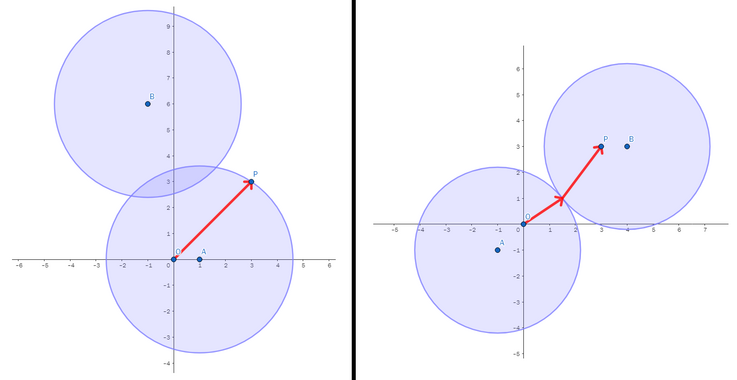Картинка, показывающая первые два набора входных данных Первая строка входных данных содержит одно целое число $$$t$$$ ($$$1 \le t \le 10^4$$$) — количество наборов входных данных.
Каждый набор входных данных состоит из трех строк:
- первая строка содержит два целых числа $$$P_x$$$ и $$$P_y$$$ ($$$-10^3 \le P_x, P_y \le 10^3$$$) — местоположение дома Монокарпа;
- вторая строка содержит два целых числа $$$A_x$$$ и $$$A_y$$$ ($$$-10^3 \le A_x, A_y \le 10^3$$$) — местоположение первого фонаря;
- третья строка содержит два целых числа $$$B_x$$$ и $$$B_y$$$ ($$$-10^3 \le B_x, B_y \le 10^3$$$) — местоположение второго фонаря.
Дополнительное ограничение на входные данные:
- в каждом наборе входных данных точки $$$O$$$, $$$P$$$, $$$A$$$ и $$$B$$$ не совпадают друг с другом.
Для каждого набора входных данных выведите ответ на отдельной строке — одно вещественное число, равное минимальному значению $$$w$$$, при котором существует полностью освещенный путь от точки $$$O$$$ до точки $$$P$$$.
Ваш ответ будет считаться правильным, если его абсолютная или относительная ошибка не превышает $$$10^{-6}$$$ — формально, если ваш ответ равен $$$a$$$, а ответ жюри равен $$$b$$$, ваш ответ будет принят, если $$$\dfrac{|a - b|}{\max(1, b)} \le 10^{-6}$$$.
23 31 0-1 63 3-1 -14 3
3.6055512755 3.2015621187
