| Codeforces Round 905 (Div. 1) |
|---|
| Закончено |
Алиса предложила Бобу сыграть в игру. Бобу эта идея не понравилась, но отказать Алисе он не смог, а потому попросил вас написать программу, которая будет играть вместо него.
Игра начинается с того, что Алиса достает клетчатый лист размера $$$n \times n$$$, клетки которого изначально не закрашены. После этого она закрашивает какие-то $$$2n$$$ различных клеток в цвета $$$1,2,\ldots, 2n$$$, соответственно, и сообщает об этих клетках Бобу.
За один ход Боб может указать на какую-то ещё не закрашенную клетку и попросить Алису закрасить эту клетку. Алиса закрашивает эту клетку в один из $$$2n$$$ цветов по своему выбору, сообщая при этом Бобу выбранный цвет. Боб может сделать не более $$$10$$$ ходов, после чего ему требуется найти хорошую четвёрку клеток.
Четвёрка клеток называется хорошей, если выполняются следующие условия:
- Все клетки из четвёрки закрашены;
- Никакие две клетки из четвёрки не раскрашены в один и тот же цвет;
- Центры клеток образуют прямоугольник, стороны которого параллельны линиям сетки.
Каждый тест состоит из нескольких наборов входных данных. Первая строка содержит одно целое число $$$t$$$ ($$$1 \le t \le 200$$$) — количество наборов входных данных. Далее следует описание наборов входных данных.
Первая строка каждого набора входных данных содержит одно целое число $$$n$$$ ($$$3 \le n \le 1000$$$) — размер поля.
$$$i$$$-я из следующих $$$2n$$$ строк содержит два целых числа $$$x_i$$$ и $$$y_i$$$ ($$$1 \le x_i, y_i \le n$$$) — координаты клетки, покрашенной в $$$i$$$-й цвет.
Гарантируется, что все координаты $$$(x_i, y_i)$$$ попарно различны для одного набора входных данных.
После считывания входных данных для каждого набора продолжите взаимодействие описанным ниже образом.
Вы можете совершить не более $$$10$$$ ходов. Чтобы сделать ход, выведите «? $$$x$$$ $$$y$$$» ($$$1 \leq x,y \leq n$$$). В ответ на это программа жюри в единственной строке выведет единственное целое число от $$$1$$$ до $$$2n$$$ — цвет клетки $$$(x,y)$$$.
После всех ходов (не обязательно делать все $$$10$$$ ходов и не обязательно делать хотя бы один ход) выведите строку в формате «! $$$x_1$$$ $$$x_2$$$ $$$y_1$$$ $$$y_2$$$» ($$$1 \leq x_1, x_2, y_1, y_2 \leq n, x_1 \ne x_2, y_1 \ne y_2$$$). Если клетки $$$(x_1, y_1)$$$, $$$(x_1, y_2)$$$, $$$(x_2, y_1)$$$, $$$(x_2, y_2)$$$ раскрашены в различные цвета, то программа жюри выведет «OK». После этого переходите к следующему набору входных данных или завершите программу, если наборов больше не осталось.
В ином случае, если какие-то из указанных клеток раскрашены в один цвет или одна из клеток ещё не раскрашена, то программа жюри выведет вам «ERROR». В таком случае ваша программа должна немедленно завершить своё исполнение, чтобы получить вердикт Неправильный ответ. В противном случае вы можете получить произвольный вердикт.
После каждого хода или ответа не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте:
- fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Обратите внимание, что интерактор является адаптивным, то есть цвет, в который Алиса будет закрашивать клетки при ходах Боба, не фиксирован заранее.
Взломы
Вы не можете делать взломы в этой задаче.
2 3 1 2 1 3 2 1 2 3 3 1 3 2 1 OK 3 1 1 1 2 1 3 2 1 2 2 2 3 OK
? 1 1 ! 1 2 1 3 ! 1 2 1 2
В первом наборе входных данных:
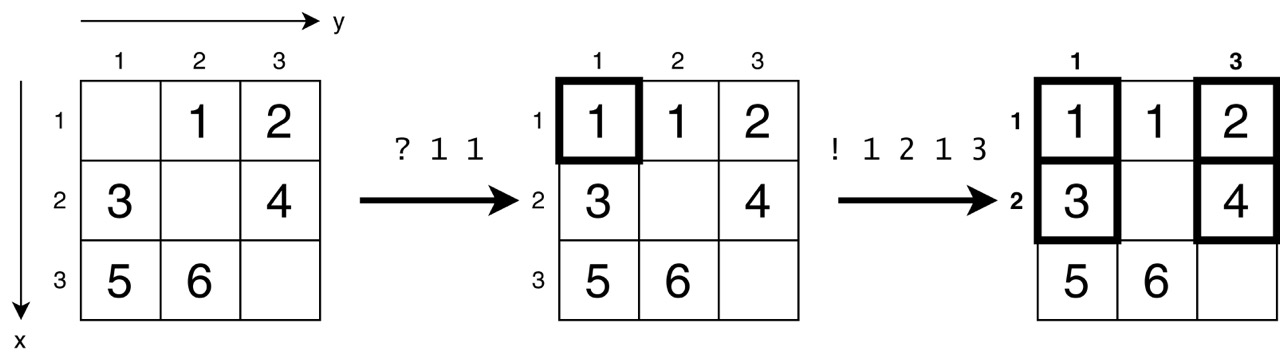
Во втором наборе входных данных клетки с координатами $$$(1, 1), (1, 2), (2, 1), (2, 2)$$$ изначально раскрашены Алисой в различные цвета.
| Название |
|---|




