Rating changes for last rounds are temporarily rolled back. They will be returned soon. ×

F. A Growing Tree
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output

You are given a rooted tree with the root at vertex $$$1$$$, initially consisting of a single vertex. Each vertex has a numerical value, initially set to $$$0$$$. There are also $$$q$$$ queries of two types:

  • The first type: add a child vertex with the number $$$sz + 1$$$ to vertex $$$v$$$, where $$$sz$$$ is the current size of the tree. The numerical value of the new vertex will be $$$0$$$.
  • The second type: add $$$x$$$ to the numerical values of all vertices in the subtree of vertex $$$v$$$.

After all queries, output the numerical value of all of the vertices in the final tree.

Input

The first line contains a single integer $$$T$$$ ($$$1 \leq T \leq 10^4$$$) — the number of test cases. The descriptions of the test cases follow.

The first line of each test case contains a single integer $$$q$$$ ($$$1 \leq q \leq 5 \cdot 10^5$$$) — the number of queries.

The following $$$q$$$ lines can fall into two cases:

  • The first type of query: The $$$i$$$-th line contains two integers $$$t_i$$$ ($$$t_i = 1$$$), $$$v_i$$$. You need to add a child with the number $$$sz + 1$$$ to vertex $$$v_i$$$, where $$$sz$$$ is the current size of the tree. It is guaranteed that $$$1 \leq v_i \leq sz$$$.
  • The second type of query: The $$$i$$$-th line contains three integers $$$t_i$$$ ($$$t_i = 2$$$), $$$v_i$$$, $$$x_i$$$ ($$$-10^9 \leq x_i \leq 10^9$$$). You need to add $$$x_i$$$ to all numerical values of vertices in the subtree of $$$v_i$$$. It is guaranteed that $$$1 \leq v_i \leq sz$$$, where $$$sz$$$ is the current size of the tree.

It is guaranteed that the sum of $$$q$$$ across all test cases does not exceed $$$5 \cdot 10^5$$$.

Output

For each test case, output the numerical value of each vertex of the final tree after all queries have been performed.

Example
Input
3
9
2 1 3
1 1
2 2 1
1 1
2 3 2
1 3
2 1 4
1 3
2 3 2
5
2 1 1
1 1
2 1 -1
1 1
2 1 1
5
1 1
1 1
2 1 1
2 1 3
2 2 10
Output
7 5 8 6 2 
1 0 1 
4 14 4
Note

In the first case, the final tree with the assigned numerical values will look like this:

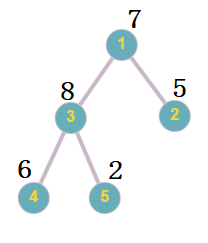The final tree with the assigned numerical values