| Codeforces Round 909 (Div. 3) |
|---|
| Закончено |
Дерево — связный граф без циклов. Можно показать, что любое дерево из $$$n$$$ вершин имеет ровно $$$n - 1$$$ ребро.
Лист — вершина в дереве, из которой выходит ровно одно ребро.
Расстояние между двумя вершинами $$$u$$$ и $$$v$$$ в дереве — минимальное количество рёбер, которое нужно пройти, чтобы из вершины $$$u$$$ прийти в вершину $$$v$$$.
У Лёши скоро день рождения, и Тимофею хотелось бы подарить ему дерево из $$$n$$$ вершин. Однако Лёша очень капризный мальчик. Каждый день на протяжении $$$q$$$ дней он будет выбирать целое число, обозначим выбранное в $$$i$$$-й день число $$$d_i$$$. Если в $$$i$$$-й день в дереве не будет двух листов на расстоянии ровно $$$d_i$$$, то Лёша будет разочарован.
Тимофей решил подарить Лёше конструктор, чтобы он сам мог менять своё дерево, как ему хочется. Тимофей знает, что Лёша ещё и ленив (ужас, а не человек), поэтому в начале каждого дня он может выполнить не более одной операции следующего вида:
- Выбрать вершины $$$u$$$, $$$v_1$$$ и $$$v_2$$$, такие, что между $$$u$$$ и $$$v_1$$$ есть ребро, а между $$$u$$$ и $$$v_2$$$ нет ребра. После этого удалить ребро между $$$u$$$ и $$$v_1$$$ и добавить ребро между $$$u$$$ и $$$v_2$$$. Эту операцию нельзя выполнить, если после неё граф перестанет быть деревом.
Чудесным образом Тимофею удалось узнать все $$$d_i$$$. После этого его посетила ещё одна гениальная мысль — на всякий случай сделать инструкцию к набору, при этом такую, чтобы Лёша не был разочарован.
Тимофей не такой ленивый, как Лёша, но когда он увидел число $$$n$$$, у него резко пропало желание разрабатывать инструкцию и придумывать изначальное дерево, поэтому он поручил эту задачу вам. Можно показать, что дерево и последовательность операций, удовлетворяющие описанным условиям, всегда существуют.
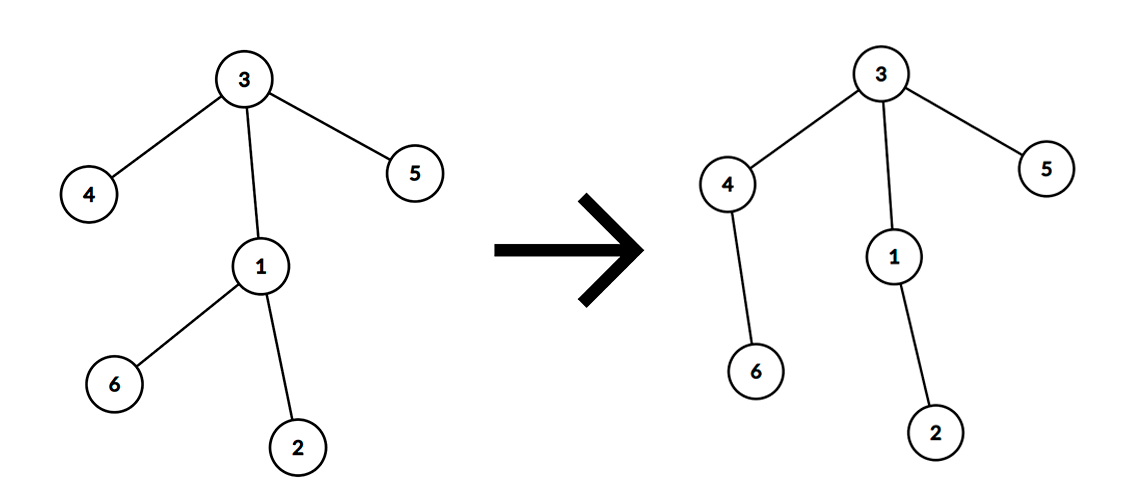
Вот пример операции, где были выбраны вершины: $$$u$$$ — $$$6$$$, $$$v_1$$$ — $$$1$$$, $$$v_2$$$ — $$$4$$$.
В первой строке дано целое число $$$t$$$ ($$$1 \leq t \leq 100$$$) — количество наборов входных данных.
В первой строке каждого набора входных данных даны целые числа $$$n$$$ ($$$3 \leq n \leq 500$$$) и $$$q$$$ ($$$1 \leq q \leq 500$$$) — количество вершин в дереве и количество дней соответственно.
В $$$i$$$-й из следующих $$$q$$$ строк дано целое число $$$d_i$$$ ($$$2 \leq d_i \leq n - 1$$$).
Гарантируется, что сумма $$$n$$$ по всем наборам входных данных не превосходит $$$500$$$. То же самое гарантируется для $$$q$$$.
Можно показать, что дерево и последовательность операций, удовлетворяющие описанным условиям, всегда существуют.
Для каждого набора входных данных сначала выведите $$$n - 1$$$ строку с описанием рёбер дерева. Если вы хотите, чтобы в дереве было ребро между вершинами $$$u$$$ и $$$v$$$, то среди этих $$$n - 1$$$ строк должна быть строка $$$v$$$ $$$u$$$ или $$$u$$$ $$$v$$$.
В следующих $$$q$$$ строках выведите по три целых числа $$$u$$$ $$$v_1$$$ $$$v_2$$$ — описание операций. Если Лёше не нужно выполнять операцию, выведите $$$-1$$$ $$$-1$$$ $$$-1$$$.
33 32225 64234324 9233222322
1 2 2 3 -1 -1 -1 -1 -1 -1 -1 -1 -1 1 2 2 3 3 4 4 5 -1 -1 -1 4 3 2 5 4 3 4 2 5 4 5 2 5 3 4 1 2 2 3 3 4 4 3 2 4 2 3 -1 -1 -1 4 3 2 -1 -1 -1 -1 -1 -1 4 2 3 4 3 2 -1 -1 -1
| Название |
|---|




